時空 解 さんの日記
2023
11月
6
(月)
09:36
本文
皆さん こんにちは、時空 解です。
今日も気を取り直して2次の問題の復習をやっています。
では今日は問題4からです。
第412回 数学検定2級2次 問題4…(模範解答は右画像)


これは模範解答を見て
「なんだ、階差数列の問題か…」
と、ちょっと呆れた次第です。
この問題が解けないのは数列の学習を疎かにしている自分だからですよね…とほほ。
これは数列の下記の公式を理解・記憶していれば解ける問題でした。

難しいのは次の問題5ですよね。
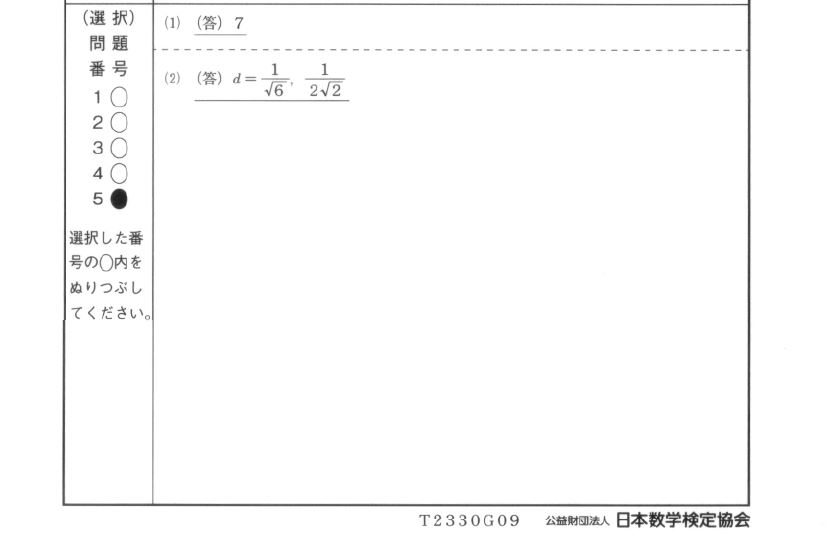
第412回 数学検定2級2次 問題5…(模範解答は右画像)

この問題。受検された方たちの "全体の正解率" がじつに 3.7 % なんです。
今回の検定で一番難しかった問題と言ってもいいでしょう。
こういう問題こそ、ここのブログで一つの解答例を示せるといいですよね…ですから昨日、チンプンカンプンだったんですが
「いやいや、夕方まで考え抜こう!」
と意気込んだんです。
結果として解けませんでしたけどね…問題文を読んでも意味が分かりませんでしたし…。( ^^;
でも、今日の朝に
「ブログの投稿を忘れた旨」
をお知らせした直後に、ピンときました!
変なもんですね。肩の力が抜けたら問題の意味が分かったんです。
まず、平面の数。
これは二つのパターンがあります。
(1) 平面 $ \alpha $ の表面側に1つの頂点。裏面に3つの頂点。
(2) 平面 $ \alpha $ の表面側に2つの頂点。裏面に2つの頂点。
それで…
(1) の場合の平面の数は、表面側に来る頂点の数は $ A,~B,~C,~D $ の4つですから $ 4 $。
(2) の場合の平面の数は、表面側に来る2つの頂点がつくる辺の組み合わせは $ {}_4 \mathrm{ C }_2 = 6 $。ここで平面の表面と裏面の区別がないので $ \displaystyle \frac{ 6 }{ 2 } = 3 $。
と言うことで平面の数の答えとしては $ 7 $ となるのでしょう。
次の距離 $ d $ について
(1) の場合の平面と頂点までの距離 $ d $ は正四面体の底面の重心 $ G $ から頂点 (例えば $ A $ ) までの距離の半分、つまり正四面体の高さの $ \displaystyle \frac{ 1 }{ 2 } $ ですから…
(高さを求めるのもなかなか難しいので、下記のサイトを参照してください)
・【3分で分かる!】正四面体の高さ・体積の求め方をわかりやすく
上記のサイトより、正四面体の高さは $ GA = \displaystyle \frac{ \sqrt{ 6 } }{ 3 } \cdot 1 $。 答えはこれの $ \displaystyle \frac{ 1 }{ 2 } $ ということになりますので $ \displaystyle \frac{ \sqrt{ 6 } }{ 6 } $。
模範解答の $ \displaystyle \frac{ 1 }{ \sqrt{ 6 } } $ は $ \displaystyle \frac{ \sqrt{ 6 } }{ 6 } $ ですから、一致しました。
(2) の場合の頂点と平面との距離 $ d $ は…うーむ…
すみません、ここで今日は時間切れとなりました。m( _ _;)m
朝の支度をして、会社に出かけないとね…。
続きはまた明日のでも…
では今日も1日の習慣を始めてます。小さな一歩・挑戦を試みています。
( ブログのコメント欄は 2022-04-16 に閉鎖いたしました )
今日も気を取り直して2次の問題の復習をやっています。
では今日は問題4からです。
第412回 数学検定2級2次 問題4…(模範解答は右画像)


これは模範解答を見て
「なんだ、階差数列の問題か…」
と、ちょっと呆れた次第です。
この問題が解けないのは数列の学習を疎かにしている自分だからですよね…とほほ。
これは数列の下記の公式を理解・記憶していれば解ける問題でした。

難しいのは次の問題5ですよね。
第412回 数学検定2級2次 問題5…(模範解答は右画像)


この問題。受検された方たちの "全体の正解率" がじつに 3.7 % なんです。
今回の検定で一番難しかった問題と言ってもいいでしょう。
こういう問題こそ、ここのブログで一つの解答例を示せるといいですよね…ですから昨日、チンプンカンプンだったんですが
「いやいや、夕方まで考え抜こう!」
と意気込んだんです。
結果として解けませんでしたけどね…問題文を読んでも意味が分かりませんでしたし…。( ^^;
でも、今日の朝に
「ブログの投稿を忘れた旨」
をお知らせした直後に、ピンときました!
変なもんですね。肩の力が抜けたら問題の意味が分かったんです。
まず、平面の数。
これは二つのパターンがあります。
(1) 平面 $ \alpha $ の表面側に1つの頂点。裏面に3つの頂点。
(2) 平面 $ \alpha $ の表面側に2つの頂点。裏面に2つの頂点。
それで…
(1) の場合の平面の数は、表面側に来る頂点の数は $ A,~B,~C,~D $ の4つですから $ 4 $。
(2) の場合の平面の数は、表面側に来る2つの頂点がつくる辺の組み合わせは $ {}_4 \mathrm{ C }_2 = 6 $。ここで平面の表面と裏面の区別がないので $ \displaystyle \frac{ 6 }{ 2 } = 3 $。
と言うことで平面の数の答えとしては $ 7 $ となるのでしょう。
次の距離 $ d $ について
(1) の場合の平面と頂点までの距離 $ d $ は正四面体の底面の重心 $ G $ から頂点 (例えば $ A $ ) までの距離の半分、つまり正四面体の高さの $ \displaystyle \frac{ 1 }{ 2 } $ ですから…
(高さを求めるのもなかなか難しいので、下記のサイトを参照してください)
・【3分で分かる!】正四面体の高さ・体積の求め方をわかりやすく
上記のサイトより、正四面体の高さは $ GA = \displaystyle \frac{ \sqrt{ 6 } }{ 3 } \cdot 1 $。 答えはこれの $ \displaystyle \frac{ 1 }{ 2 } $ ということになりますので $ \displaystyle \frac{ \sqrt{ 6 } }{ 6 } $。
模範解答の $ \displaystyle \frac{ 1 }{ \sqrt{ 6 } } $ は $ \displaystyle \frac{ \sqrt{ 6 } }{ 6 } $ ですから、一致しました。
(2) の場合の頂点と平面との距離 $ d $ は…うーむ…
すみません、ここで今日は時間切れとなりました。m( _ _;)m
朝の支度をして、会社に出かけないとね…。
続きはまた明日のでも…
では今日も1日の習慣を始めてます。小さな一歩・挑戦を試みています。
( ブログのコメント欄は 2022-04-16 に閉鎖いたしました )
閲覧(6448)
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |





 前の日記
前の日記



