時空 解 さんの日記
2023
11月
8
(水)
09:44
本文
皆さん こんにちは、時空 解です。
今日は尻切れトンボになっていた問題5を最後までやってみます。
第412回 数学検定2級2次 問題5…(模範解答は右画像)

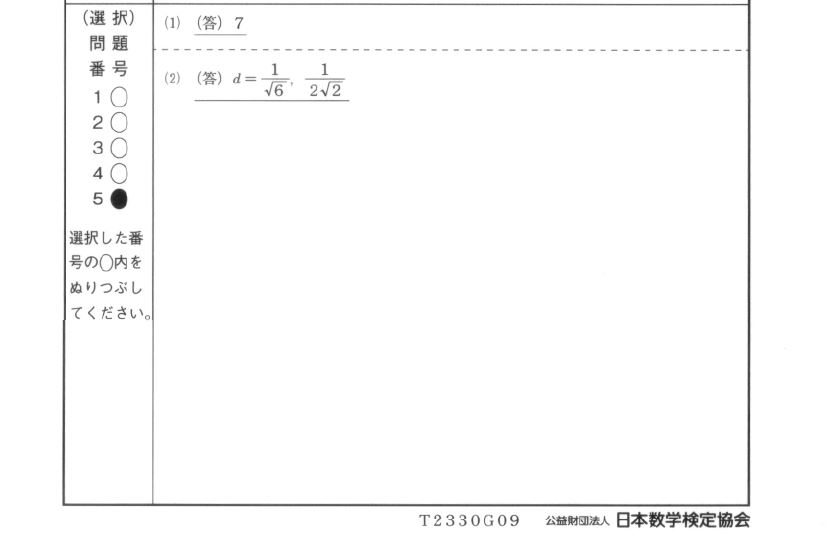
まずは (1) の "平面の数" についてですが…
この問題は "等距離にある平面" と言うものを丁寧に (?)
「点 $ P $ と平面 $ \alpha $ の距離 $ d $ を以下のように定めます。」
と宣言して、線分 $ PH $ を距離 $ d $ と定めていますよね。
これって、個人的には不必要な気がしますが、…皆さんはどう思われました? ( ^^;
ただ単に設問 (1) に書かれていとおり
「各頂点からの距離が等しい平面」
で十分な気がしますが…。
上記のような余計な "定め " がこの問題5を難しい感じにしています…検定のときには面喰いました。
でも、今となってはこの "定め" を
「丁寧に書かれている問題だなぁ…」
くらいに想えないといけないのかも知れません。これも数学力のうちの一つかもね。
まぁそんなことはともかく…「各頂点からの距離が等しい平面」は、二日前のブログにも書いたとおり
(a) 平面 $ \alpha $ の表面側に1つの頂点。裏面に3つの頂点。
(b) 平面 $ \alpha $ の表面側に2つの頂点。裏面に2つの頂点。
の二つのパターンがありますよね。
結果として平面の数は $ 7 $ となります。
(詳細は二日前のブログ記事参照してくださいね。2023年11月06日)
次に設問 (2) の距離 $ d $ についてですが…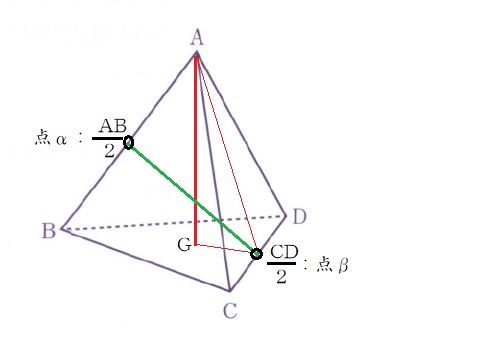
まずは平面がパターン (a) の場合の距離は、右画像の赤の線分 $ AG $ の $ \displaystyle \frac{ 1 }{ 2 } $。
平面がパターン (b) の場合の距離は、右画像の緑の線分 $ α β $ の $ \displaystyle \frac{ 1 }{ 2 } $。
となることは分かりますよね。
線分 $ AG $ は直角3角形 $ AG β $ ( $ \angle AG β = 90^\circ $ ) にピタゴラスの定理を適用すれば計算できます。
$ G $ は正3角形 $ BCD $ の重心ですからね。ですから線分 $ βG $ は線分 $ β G $ の $ \displaystyle \frac{ 1 }{ 3 } $ ですからね…。それと線分 $ A β $ は一辺が $ 1 $ の正3角形を垂直に切っている線分ですからね、あとは計算できますよね。
線分 $ α β $ も直角3角形 $ A α β $ ( $ \angle A α β = 90^\circ $ ) にピタゴラスの定理を適用すれば計算できます。
線分 $ A α $ は $ \displaystyle \frac{ 1 }{ 2 } $ です。
右画像が頭の中に描ける方ならば、この設問 (2) は簡単に解けますね…。
でも手書きができる人さえも、なかなかいないのが実態なのかもしれませんね。
検定のデータとして "全体の正答率 $=3.7% $ がそれを物語っています。
おっと、今日もまた時間が掛かってしまいました。
次の問題6、7についてはまた明日以降になります…すみません。m( _ _ )m
では今日も1日の習慣を始めてます。小さな一歩・挑戦を試みています。
( ブログのコメント欄は 2022-04-16 に閉鎖いたしました )
今日は尻切れトンボになっていた問題5を最後までやってみます。
第412回 数学検定2級2次 問題5…(模範解答は右画像)


まずは (1) の "平面の数" についてですが…
この問題は "等距離にある平面" と言うものを丁寧に (?)
「点 $ P $ と平面 $ \alpha $ の距離 $ d $ を以下のように定めます。」
と宣言して、線分 $ PH $ を距離 $ d $ と定めていますよね。
これって、個人的には不必要な気がしますが、…皆さんはどう思われました? ( ^^;
ただ単に設問 (1) に書かれていとおり
「各頂点からの距離が等しい平面」
で十分な気がしますが…。
上記のような余計な "定め " がこの問題5を難しい感じにしています…検定のときには面喰いました。
でも、今となってはこの "定め" を
「丁寧に書かれている問題だなぁ…」
くらいに想えないといけないのかも知れません。これも数学力のうちの一つかもね。
まぁそんなことはともかく…「各頂点からの距離が等しい平面」は、二日前のブログにも書いたとおり
(a) 平面 $ \alpha $ の表面側に1つの頂点。裏面に3つの頂点。
(b) 平面 $ \alpha $ の表面側に2つの頂点。裏面に2つの頂点。
の二つのパターンがありますよね。
結果として平面の数は $ 7 $ となります。
(詳細は二日前のブログ記事参照してくださいね。2023年11月06日)
次に設問 (2) の距離 $ d $ についてですが…

まずは平面がパターン (a) の場合の距離は、右画像の赤の線分 $ AG $ の $ \displaystyle \frac{ 1 }{ 2 } $。
平面がパターン (b) の場合の距離は、右画像の緑の線分 $ α β $ の $ \displaystyle \frac{ 1 }{ 2 } $。
となることは分かりますよね。
線分 $ AG $ は直角3角形 $ AG β $ ( $ \angle AG β = 90^\circ $ ) にピタゴラスの定理を適用すれば計算できます。
$ G $ は正3角形 $ BCD $ の重心ですからね。ですから線分 $ βG $ は線分 $ β G $ の $ \displaystyle \frac{ 1 }{ 3 } $ ですからね…。それと線分 $ A β $ は一辺が $ 1 $ の正3角形を垂直に切っている線分ですからね、あとは計算できますよね。
線分 $ α β $ も直角3角形 $ A α β $ ( $ \angle A α β = 90^\circ $ ) にピタゴラスの定理を適用すれば計算できます。
線分 $ A α $ は $ \displaystyle \frac{ 1 }{ 2 } $ です。
右画像が頭の中に描ける方ならば、この設問 (2) は簡単に解けますね…。
でも手書きができる人さえも、なかなかいないのが実態なのかもしれませんね。
検定のデータとして "全体の正答率 $=3.7% $ がそれを物語っています。
おっと、今日もまた時間が掛かってしまいました。
次の問題6、7についてはまた明日以降になります…すみません。m( _ _ )m
では今日も1日の習慣を始めてます。小さな一歩・挑戦を試みています。
( ブログのコメント欄は 2022-04-16 に閉鎖いたしました )
閲覧(3026)
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |





 前の日記
前の日記



