時空 解 さんの日記
2023
11月
9
(木)
13:25
本文
皆さん こんにちは、時空 解です。
さっそく2次の必須問題である問題6を見てゆきましょう。
第412回 数学検定2級2次 問題6…(模範解答は右画像)


この問題。…実は振り返ってみて分かったことなんですが、設問 (1) は答えられなくてはいけなかった問題でした…。
設問 (1) の与式に定数 $ k $ が入っていますよね?この $ k $ が無かったとしたら…。
きっと検定中にでも解けていたことでしょう。
下記に $ k $ がない場合の問題を書いてみましょう。
この問題、(1) の不等式ならば解くのは簡単です。
なんといっても2次方程式の解の公式を使って $ x $ の値がでてきますからね。
でも、もともとの問題には $ k $ が入っているので
「あれ? この問題ってどんな問題だ … $ k $、$ k $, ケイッ…?」
と、なんだか頭の中が "数の森、変数の霧" の中に迷い込んでしまったんです。
まぁこんなふうになる自分は、数学の実力のなさを露呈しているんですけどね。_| ̄|○
(こんな私事はともかく…)
ともかく
$ x^2 -2x -4 \lt 0 $
は左辺を因数分解すると
$ \{x +(1 + \sqrt{ 5 } ) \}\{x +(1 - \sqrt{ 5 } ) \} \lt 0 $
です。
ですから $ x $ の範囲は、2次方程式のグラフが下に凸なので
$ (1 - \sqrt{ 5 } ) \lt x \lt (1 + \sqrt{ 5 } ) $
だとわかります。
ここまでできれば、もう頭の中は "数の森、変数の霧" から抜け出てきました。
改めて問題6の与式 (1) を見てみると
$ x^2 -2kx +k^2 -4 \lt 0 $ にでてくる $ k^2 -4 $ は $ (k +2)(k -2) $ です。
これも左辺は因数分解できすよね。因数分解すると
$ \{ x +(k+2) \} \{ x +(k-2) \} \lt 0 $
となって、$ (k+2) \gt (k-2) $ なので $ x $ の範囲は
$ k-2 \lt x \lt k+2 $
ですよね。
これで模範解答と同じ答えになりました。
うーむ…
少なくともこの問題、設問 (1) だけでも解けなくてはいけなかったです。残念…。
ところで、ちょっとわかりにくいのが設問 (2) ですよね。
これはきっちりとグラフが頭の中に描けるか否か。(1) と (2) のグラフの位置関係がちゃんと把握できるか、です。
模範解答を見てみても、なんだかどうしてこれでいいのやら分からなかった私なんですが、グラフを描いてみてやっと納得できました。
そのグラフを動画として「数検の必勝アイテム」にアップしておきました。
第412回 数学検定2級2次 問題6
たった 18秒たらずの動画ですが、ぜひ視聴してみてください。
$ k $ の取りうる範囲は、2つのグラフがそれぞれ下記の2つの位置関係にいるところですよね。
(a)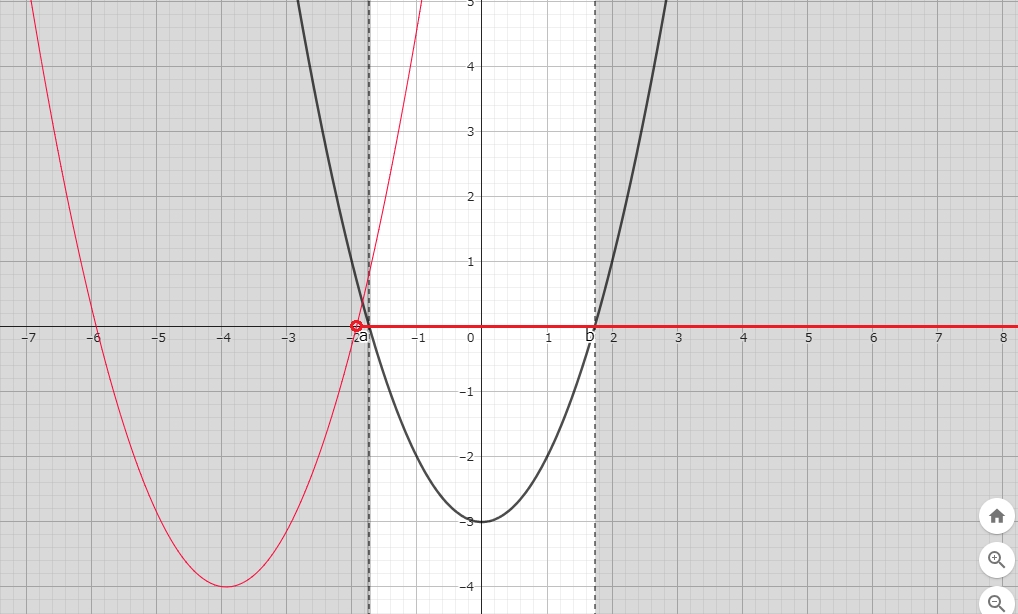 (b)
(b)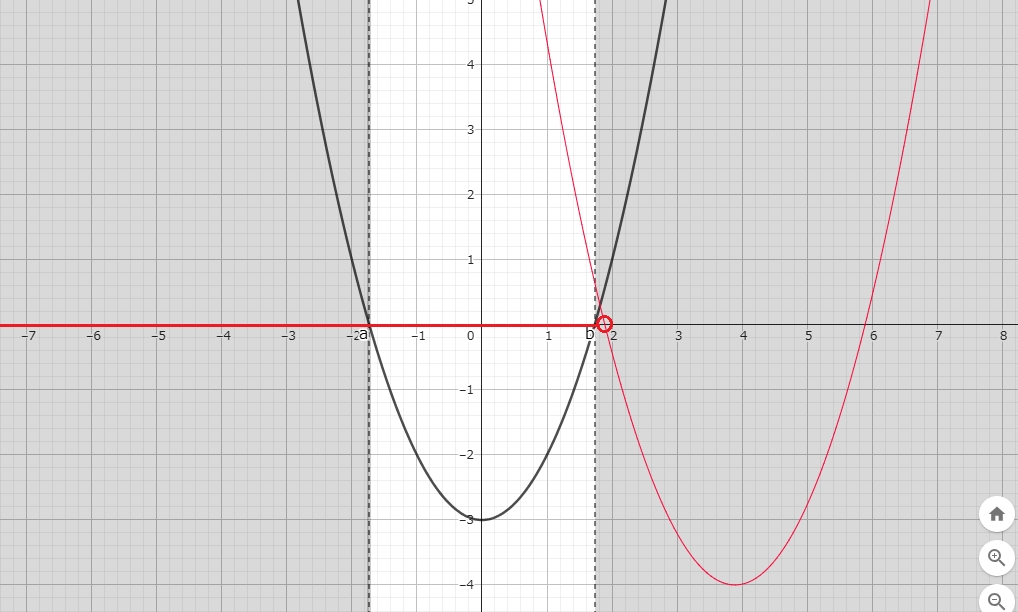
赤いグラフが $ - \sqrt{ 3 } \lt x \lt \sqrt{ 3 } $ である白の領域から
(a) 左側に来るときの $ k $ の範囲のイメージ。
(1) を満たすすべての実数について、(2) が赤いグラフの右側で成立している。
(b) 右側に来るときの $ k $ の範囲のイメージ。
(1) を満たすすべての実数について、(2)が赤いグラフの左側で成立している。
これが設問 (2) の答に繋がるイメージです…。
このイメージが頭の中になかなか浮かばない私です。_| ̄|○
このイメージを持って $ k $ の範囲を不等式で表したのが模範解答ですよね…こんなふうに記述・表現するんですね。
では、明日には問題7をやってゆきますね。今日はここまでといたします。
では今日も休日を始めています。休日の充実こそ、人生の充実です。
( ブログのコメント欄は 2022-04-16 に閉鎖いたしました )
さっそく2次の必須問題である問題6を見てゆきましょう。
第412回 数学検定2級2次 問題6…(模範解答は右画像)


この問題。…実は振り返ってみて分かったことなんですが、設問 (1) は答えられなくてはいけなかった問題でした…。
設問 (1) の与式に定数 $ k $ が入っていますよね?この $ k $ が無かったとしたら…。
きっと検定中にでも解けていたことでしょう。
下記に $ k $ がない場合の問題を書いてみましょう。
問題
$ x $ に関する2つの2次方程式
$ x^2 -2x -4 \lt 0 $ … (1)
$ x^2 -3 \gt 0 $ … (2)
について、次の問いに答えなさい。
(1) (1) の不等式を解きなさい。この問題は解法の過程を記述せずに、答えだけを書いてください。
(2) --- ( $ k $ がないので設問が成立しない )
$ x $ に関する2つの2次方程式
$ x^2 -2x -4 \lt 0 $ … (1)
$ x^2 -3 \gt 0 $ … (2)
について、次の問いに答えなさい。
(1) (1) の不等式を解きなさい。この問題は解法の過程を記述せずに、答えだけを書いてください。
(2) --- ( $ k $ がないので設問が成立しない )
この問題、(1) の不等式ならば解くのは簡単です。
なんといっても2次方程式の解の公式を使って $ x $ の値がでてきますからね。
でも、もともとの問題には $ k $ が入っているので
「あれ? この問題ってどんな問題だ … $ k $、$ k $, ケイッ…?」
と、なんだか頭の中が "数の森、変数の霧" の中に迷い込んでしまったんです。
まぁこんなふうになる自分は、数学の実力のなさを露呈しているんですけどね。_| ̄|○
(こんな私事はともかく…)
ともかく
$ x^2 -2x -4 \lt 0 $
は左辺を因数分解すると
$ \{x +(1 + \sqrt{ 5 } ) \}\{x +(1 - \sqrt{ 5 } ) \} \lt 0 $
です。
ですから $ x $ の範囲は、2次方程式のグラフが下に凸なので
$ (1 - \sqrt{ 5 } ) \lt x \lt (1 + \sqrt{ 5 } ) $
だとわかります。
ここまでできれば、もう頭の中は "数の森、変数の霧" から抜け出てきました。
改めて問題6の与式 (1) を見てみると
$ x^2 -2kx +k^2 -4 \lt 0 $ にでてくる $ k^2 -4 $ は $ (k +2)(k -2) $ です。
これも左辺は因数分解できすよね。因数分解すると
$ \{ x +(k+2) \} \{ x +(k-2) \} \lt 0 $
となって、$ (k+2) \gt (k-2) $ なので $ x $ の範囲は
$ k-2 \lt x \lt k+2 $
ですよね。
これで模範解答と同じ答えになりました。
うーむ…
少なくともこの問題、設問 (1) だけでも解けなくてはいけなかったです。残念…。
ところで、ちょっとわかりにくいのが設問 (2) ですよね。
これはきっちりとグラフが頭の中に描けるか否か。(1) と (2) のグラフの位置関係がちゃんと把握できるか、です。
模範解答を見てみても、なんだかどうしてこれでいいのやら分からなかった私なんですが、グラフを描いてみてやっと納得できました。
そのグラフを動画として「数検の必勝アイテム」にアップしておきました。
第412回 数学検定2級2次 問題6
たった 18秒たらずの動画ですが、ぜひ視聴してみてください。
$ k $ の取りうる範囲は、2つのグラフがそれぞれ下記の2つの位置関係にいるところですよね。
(a)
 (b)
(b)
赤いグラフが $ - \sqrt{ 3 } \lt x \lt \sqrt{ 3 } $ である白の領域から
(a) 左側に来るときの $ k $ の範囲のイメージ。
(1) を満たすすべての実数について、(2) が赤いグラフの右側で成立している。
(b) 右側に来るときの $ k $ の範囲のイメージ。
(1) を満たすすべての実数について、(2)が赤いグラフの左側で成立している。
これが設問 (2) の答に繋がるイメージです…。
このイメージが頭の中になかなか浮かばない私です。_| ̄|○
このイメージを持って $ k $ の範囲を不等式で表したのが模範解答ですよね…こんなふうに記述・表現するんですね。
では、明日には問題7をやってゆきますね。今日はここまでといたします。
では今日も休日を始めています。休日の充実こそ、人生の充実です。
( ブログのコメント欄は 2022-04-16 に閉鎖いたしました )
閲覧(6322)
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |





 前の日記
前の日記



