時空 解 さんの日記
2023
11月
11
(土)
09:20
本文
皆さん こんにちは、時空 解です。
今日も2次検定問題の検討、復習をして行こうと思います。
今回で最終問題、必須問題である問題7です。
第412回 数学検定2級2次 問題7…(模範解答は右画像)


うーむ…この問題も模範解答をみてみたら…
出来なければいけなかった問題。_| ̄|○
この問題って「新課程 青チャート式数学II」の、例えば基本例題223とか…
・やっと理解できました。「新課程 青チャート式数学II」基本例題223 (改訂版では 213)
例えば重要例題224とか。
・場合分けに四苦八苦した問題。「新課程 青チャート数学II」重要例題224 (改訂版では 214)
この必須問題7は3次方程式の増減を調べ、定義域内の最大値を求めれば良い問題なんです。
ただ、設問 (1) でもある3次方程式が立てられないと解けません。(まぁ当たり前ですが…)
なんと言っても私はこれ (3次方程式を立てること) ができなかったのです。
2次検定がスタートした時に、初めに必須問題の6と7を眺めたんですよね…それで
「うーむ…両方とも解法がピンとこない…」
と、"自分には解けない問題" と言う思い込みを抱いてしまった…。
でも落ち着いてみてみるとわかる問題だったんです…悔しい…
3次方程式を立てるには、問題で示されている正四角柱の体積を $ V $、 "高さ" を $ h $ とでも置けばいいですよね。
この $ V $ を求める3次方程式、つまり設問 (1) の答えが求められれば、あとはもう「青チャート式数学II」の基本例題223、重要例題224のようにやればいいですよね。
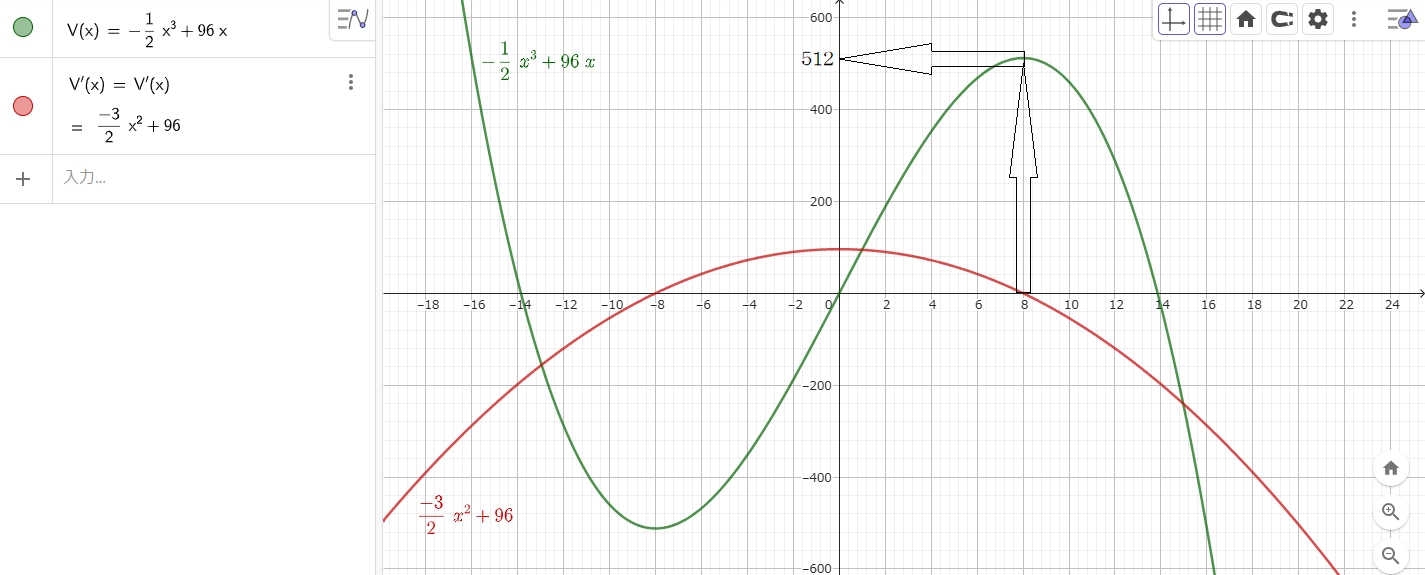
つまり
・3次方程式の微分をとって極値を求める
これです。(右画像参照)
おつと、その前に定義域を確認しておかないといけなかったですね。m( _ _ )m
この定義域は簡単です。
正四角柱の $ x $ の長さの最大と最小は、ペッタンコと背高のっぽですよね。
まぁ2次検定を受けているときには、このことにすら気が付かなかったんですけどね…私。( ^^;
と言うことで、この必須問題7の答えは $ 512 $ と求められるのです…。
うーむ…今回の2次検定…振り返ってみると7問中4つは解けても良い問題…?
いやいや、現実は解くどころか
「…わからん _| ̄|○」
と、初めから諦めているような状態だった…
「自分は数学が得意だ」と、想っていた頃が懐かしいですね。
…自惚れではなく本当の実力を身に着けたいものです。
では今日も1日の習慣を始めてます。小さな一歩・挑戦を試みています。
( ブログのコメント欄は 2022-04-16 に閉鎖いたしました )
今日も2次検定問題の検討、復習をして行こうと思います。
今回で最終問題、必須問題である問題7です。
第412回 数学検定2級2次 問題7…(模範解答は右画像)


うーむ…この問題も模範解答をみてみたら…
出来なければいけなかった問題。_| ̄|○
この問題って「新課程 青チャート式数学II」の、例えば基本例題223とか…
・やっと理解できました。「新課程 青チャート式数学II」基本例題223 (改訂版では 213)
例えば重要例題224とか。
・場合分けに四苦八苦した問題。「新課程 青チャート数学II」重要例題224 (改訂版では 214)
この必須問題7は3次方程式の増減を調べ、定義域内の最大値を求めれば良い問題なんです。
ただ、設問 (1) でもある3次方程式が立てられないと解けません。(まぁ当たり前ですが…)
なんと言っても私はこれ (3次方程式を立てること) ができなかったのです。
2次検定がスタートした時に、初めに必須問題の6と7を眺めたんですよね…それで
「うーむ…両方とも解法がピンとこない…」
と、"自分には解けない問題" と言う思い込みを抱いてしまった…。
でも落ち着いてみてみるとわかる問題だったんです…悔しい…
3次方程式を立てるには、問題で示されている正四角柱の体積を $ V $、 "高さ" を $ h $ とでも置けばいいですよね。
・正四角柱の "表面積の方程式" を立てる。
底面は一辺の長さが $ x $ だから $ x^2 $。
天井面も同じ $ x^2 $。
高さを $ h $ とすると、4面ある側面は $ (x × h) × 4 $。
ここで表面積は $ 384 $ なのだから
$ 384 = (x^2) × 2 + (x × h) × 4 = 2x^2 + 4hx $
$ \therefore h = \displaystyle \frac{ 96 }{ x } - \frac{ 1 }{ 2 } x $ …(a)
・正四角柱の "体積の方程式" を立てる。
$ V = x^2 × h $ …(b)
上記 (a),(b) 2つを連立方程式として、高さ $ h $ を消去して $ V $ を求めればいいんですよね。
$ V = x^2 × \left( \displaystyle \frac{ 96 }{ x } - \frac{ 1 }{ 2 } x \right) $
式を整理して
$ V = - \displaystyle \frac{ 1 }{ 2 } x^3 + 96x $
底面は一辺の長さが $ x $ だから $ x^2 $。
天井面も同じ $ x^2 $。
高さを $ h $ とすると、4面ある側面は $ (x × h) × 4 $。
ここで表面積は $ 384 $ なのだから
$ 384 = (x^2) × 2 + (x × h) × 4 = 2x^2 + 4hx $
$ \therefore h = \displaystyle \frac{ 96 }{ x } - \frac{ 1 }{ 2 } x $ …(a)
・正四角柱の "体積の方程式" を立てる。
$ V = x^2 × h $ …(b)
上記 (a),(b) 2つを連立方程式として、高さ $ h $ を消去して $ V $ を求めればいいんですよね。
$ V = x^2 × \left( \displaystyle \frac{ 96 }{ x } - \frac{ 1 }{ 2 } x \right) $
式を整理して
$ V = - \displaystyle \frac{ 1 }{ 2 } x^3 + 96x $
この $ V $ を求める3次方程式、つまり設問 (1) の答えが求められれば、あとはもう「青チャート式数学II」の基本例題223、重要例題224のようにやればいいですよね。

つまり
・3次方程式の微分をとって極値を求める
これです。(右画像参照)
おつと、その前に定義域を確認しておかないといけなかったですね。m( _ _ )m
この定義域は簡単です。
正四角柱の $ x $ の長さの最大と最小は、ペッタンコと背高のっぽですよね。
・正四角柱が限りなくペッタンコで、表面積 $ 384 $ がほとんど底面と天井面の二つに偏っている場合。 これが定義域 $ x $ の最大 (最長) 値。
$ 384 \approx 2x^2 $
上記を解くと $ x = \pm 8 \sqrt{ 3 } $
・正四角柱が限りなく背高のっぽ。 これが定義域 $ x $ の最小値。
$ x \approx 0 $
したがって、定義域は $ 0 \lt x \lt 8 \sqrt{ 3 } $
$ 384 \approx 2x^2 $
上記を解くと $ x = \pm 8 \sqrt{ 3 } $
・正四角柱が限りなく背高のっぽ。 これが定義域 $ x $ の最小値。
$ x \approx 0 $
したがって、定義域は $ 0 \lt x \lt 8 \sqrt{ 3 } $
まぁ2次検定を受けているときには、このことにすら気が付かなかったんですけどね…私。( ^^;
と言うことで、この必須問題7の答えは $ 512 $ と求められるのです…。
うーむ…今回の2次検定…振り返ってみると7問中4つは解けても良い問題…?
いやいや、現実は解くどころか
「…わからん _| ̄|○」
と、初めから諦めているような状態だった…
「自分は数学が得意だ」と、想っていた頃が懐かしいですね。
…自惚れではなく本当の実力を身に着けたいものです。
では今日も1日の習慣を始めてます。小さな一歩・挑戦を試みています。
( ブログのコメント欄は 2022-04-16 に閉鎖いたしました )
閲覧(6312)
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |





 前の日記
前の日記



