皆さん こんにちは、時空 解です。

今日は (も？) ボヤキなのでご了承ください…。m( _ _;)m

朝から下記の問題を考えて (はたからすれば、見ていただけの状態かも…) いたのですが。
 
(1) はまぁ解法はわかりますよね。
これは
縦に　　グー、チョキ、パー
横にも　グー、チョキ、パー
を並べて、表を作ればいいですよね。で、勝負が決まるところに○、決まらないところに△を書けば納得の行く答えが出せます。

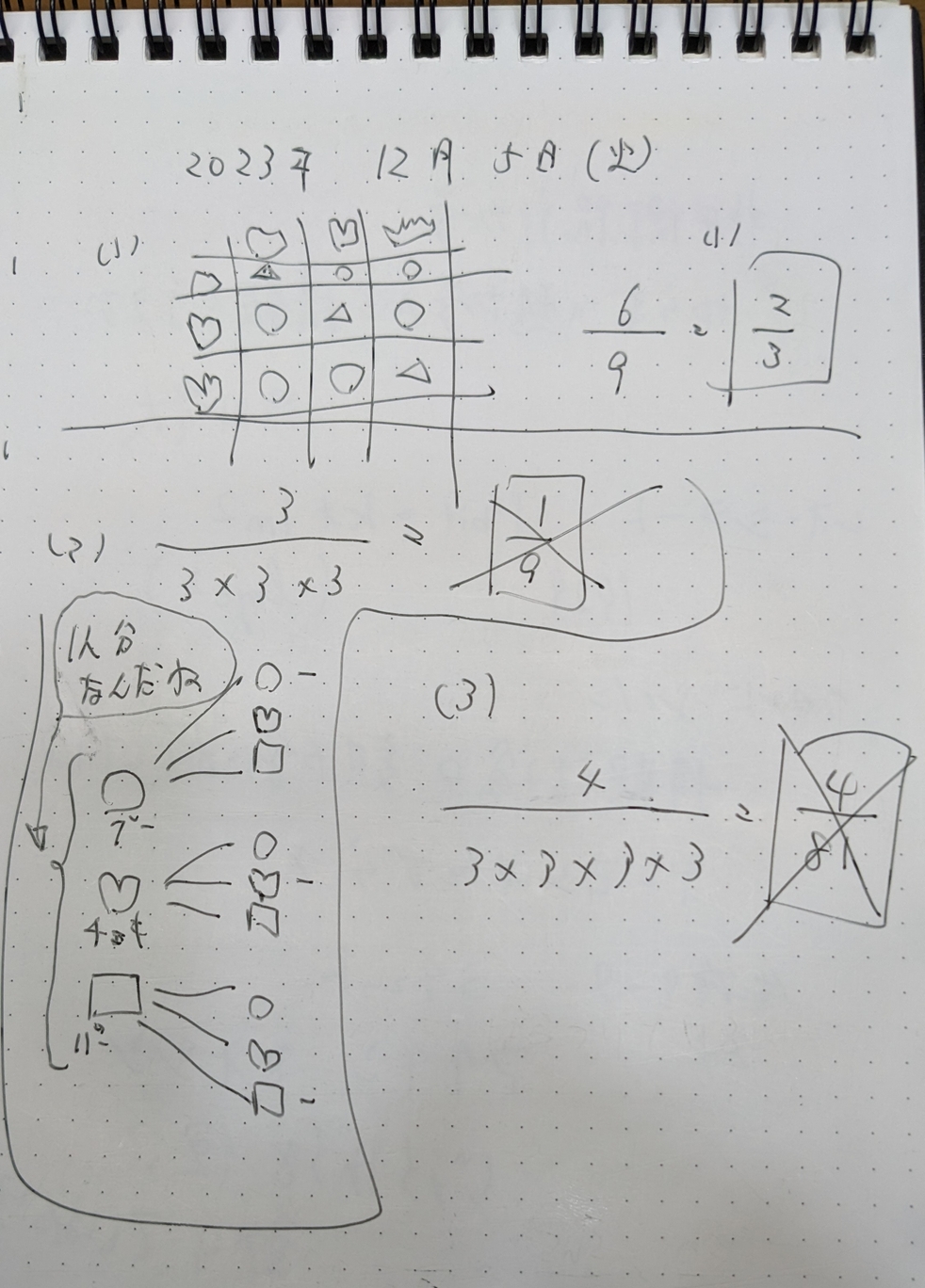
でもね、設問(2) をどう考えたら良いのかなかなか分かりませんでした。
でも、これは樹形図を描いてみれば見えてくると気が付いたのですが…

その結果、私が出した結論は $ \displaystyle \frac{ 1 }{ 9 } $
これで正しいだろうと、ほくそ笑みながら解答を見てみると…

ガガーン！　　　$ \displaystyle \frac{ 1 }{ 3 } $　…どうして？　

でも青チャート数学Ａの解説動画を視聴して、私が考えていなかった点がわかりました。
「誰が勝つか　と　どの手を出すのか」
これは分けて考えないといけないのだと言うことなんですね。
これが分かっていなかったから、樹形図も
「どの手を出すのか」
のみのものとなって、 $ \displaystyle \frac{ 1 }{ 9 } $ となってしまったのです。

樹形図に「誰がかつのか」と言うことも考慮しないと正しい答えが出てこないと言うことです。

設問(3) についてもしっかりと理解したいところですが、今日はもう時間となってしまいました。
また明日にでも解説動画を視聴して $ \displaystyle \frac{ 4! }{ 2! } $ の意味を理解したいと思います。


では今日も１日の習慣を始めてます。小さな一歩・挑戦を試みています。
☆ 夜もブログ投稿を始めました。"夜にもブログ NOW" (2023年 11月20日 ～)
中身はないけどね。悪しき夜の習慣 撲滅運動です。