時空 解 さんの日記
2024
1月
4
(木)
10:52
本文
皆さん こんにちは、時空 解です。
今日は休日。充実した人生の日々とはどんなものかをシミュレートできる日です。
今日は今年に入って初めての休日となりました。
頑張って休日を充実させて行きたいところです。休日を思い通りに過ごすことができて、しかも思い通りの行動から収入が得られるのなら幸せですよね。
と言うことで、今日も朝から数学の学習を行っていました。
数学の問題はスッキリと解くことができ、それが自分なりのオリジナリティーに溢れていればいいのですけどね。
今回解いてみた問題は
「新課程 青チャート式数学II」基本例題229
です。
この問題は微分を利用して3次不等式、4次不等式の証明を行うものです。
問題の解法自体にアイディアが有るいい問題です。
ですから私のオリジナリティーなんてお呼びでない、と言ったところです。
(今日もオリジナリティーは披露できませんが、悪しからず。m( _ _ )m )
この「新課程 青チャート式数学II」基本例題229 不等式の証明 (微分利用)
(答えは解説動画 (1) , (2) を参照ください)
初見でいきなり数検などで見たら途方もなく時間を浪費させられるも問題でしょう。
問題の解法のポイントは
グラフの形を検討する (極値を調べる)
と言う方針ですよね。
微分を使って、グラフの極大値・極小値を見定めて、不等式を証明する…と言う発想は面白いですよね。
でも設問 (2) の4次不等式
$ x^4 - 16 \geqq 32(x-2) $
ともなると、グラフのイメージもつかみにくいです。
微分方程式は $ f'(x) = 4(x-2)(x^2 +2x +4) $ となって、極値点は $ x = 2 $ と それに虚数ですよね…
$ x^2 +2x +4 = (x+1)^2 +3 $
これを解くと
$ (x+1)^2 = -3 $
$ x+1 = \pm \sqrt{ -3 } $
つまり $ x = \pm \sqrt{ 3 } i - 1 $
ですからね。
これだと4次方程式のグラフの極値がどこなのかチンプンカンプンです。( ^^;
でもこの虚数解は求めなくても、グラフの形は見通しが付けられる、と言うことですよね。
ここがこの設問 (2) のポイント。
$ (x+1)^2 +3 \gt 0 $
ですからね。
虚数解の解釈がわからないと証明した気分になれないんですよ。でも常に $ (x+1)^2 +3 $ が正なので、極値に関係するのは
$ f'(x) = 4(x-2)(x^2 +2x +4) $
のうちの
$ (x -2) $
の部分だけと分かります。
一応、グラフを示しておきます。
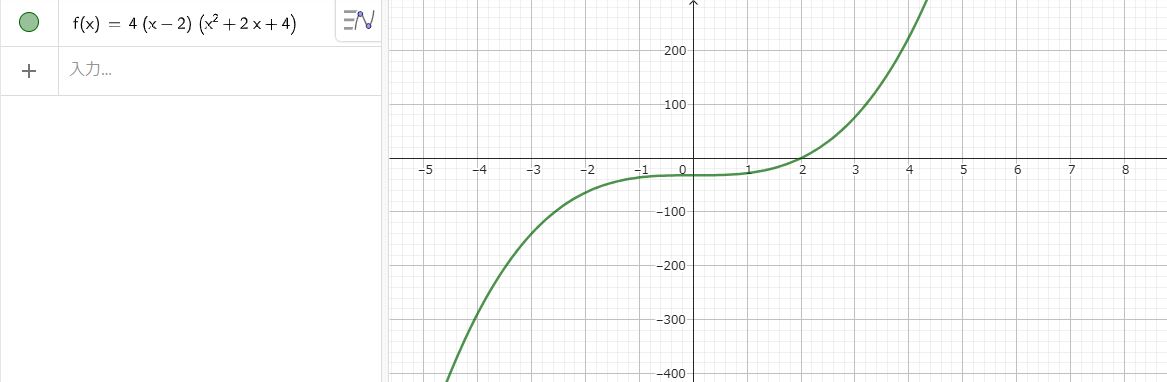
これで私はスッキリしました。
では今日も休日を始めています。休日の充実こそ、人生の充実です。
今日は休日。充実した人生の日々とはどんなものかをシミュレートできる日です。
今日は今年に入って初めての休日となりました。
頑張って休日を充実させて行きたいところです。休日を思い通りに過ごすことができて、しかも思い通りの行動から収入が得られるのなら幸せですよね。
と言うことで、今日も朝から数学の学習を行っていました。
数学の問題はスッキリと解くことができ、それが自分なりのオリジナリティーに溢れていればいいのですけどね。
今回解いてみた問題は
「新課程 青チャート式数学II」基本例題229
です。
この問題は微分を利用して3次不等式、4次不等式の証明を行うものです。
問題の解法自体にアイディアが有るいい問題です。
ですから私のオリジナリティーなんてお呼びでない、と言ったところです。
(今日もオリジナリティーは披露できませんが、悪しからず。m( _ _ )m )
この「新課程 青チャート式数学II」基本例題229 不等式の証明 (微分利用)
次の不等式が成り立つことを証明せよ。
(1) $ x \gt 2 $ のとき $ x^3 + 16 \gt 12x $
(2) $ x \gt 0 $ のとき $ x^4 -16 \geqq 32(x -2) $
(1) $ x \gt 2 $ のとき $ x^3 + 16 \gt 12x $
(2) $ x \gt 0 $ のとき $ x^4 -16 \geqq 32(x -2) $
(答えは解説動画 (1) , (2) を参照ください)
初見でいきなり数検などで見たら途方もなく時間を浪費させられるも問題でしょう。
問題の解法のポイントは
グラフの形を検討する (極値を調べる)
と言う方針ですよね。
微分を使って、グラフの極大値・極小値を見定めて、不等式を証明する…と言う発想は面白いですよね。
でも設問 (2) の4次不等式
$ x^4 - 16 \geqq 32(x-2) $
ともなると、グラフのイメージもつかみにくいです。
微分方程式は $ f'(x) = 4(x-2)(x^2 +2x +4) $ となって、極値点は $ x = 2 $ と それに虚数ですよね…
$ x^2 +2x +4 = (x+1)^2 +3 $
これを解くと
$ (x+1)^2 = -3 $
$ x+1 = \pm \sqrt{ -3 } $
つまり $ x = \pm \sqrt{ 3 } i - 1 $
ですからね。
これだと4次方程式のグラフの極値がどこなのかチンプンカンプンです。( ^^;
でもこの虚数解は求めなくても、グラフの形は見通しが付けられる、と言うことですよね。
ここがこの設問 (2) のポイント。
$ (x+1)^2 +3 \gt 0 $
ですからね。
虚数解の解釈がわからないと証明した気分になれないんですよ。でも常に $ (x+1)^2 +3 $ が正なので、極値に関係するのは
$ f'(x) = 4(x-2)(x^2 +2x +4) $
のうちの
$ (x -2) $
の部分だけと分かります。
一応、グラフを示しておきます。

これで私はスッキリしました。
では今日も休日を始めています。休日の充実こそ、人生の充実です。
閲覧(3443)
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |





 前の日記
前の日記



