時空 解 さんの日記
2024
3月
5
(火)
09:24
本文
皆さん こんにちは、時空 解です。
定積分を利用して、複数のグラフに囲まれた部分の面積を求める問題。
高校時代には…
おっと!
まぁ高校時代のことは書くのは止めましょうね。
けっきょく何時もと同じことですから…
(気持ちを切り変えて)
面積を求める問題に関して注意する点は、符号ですよね。
下記の問題でそれを実感しました。
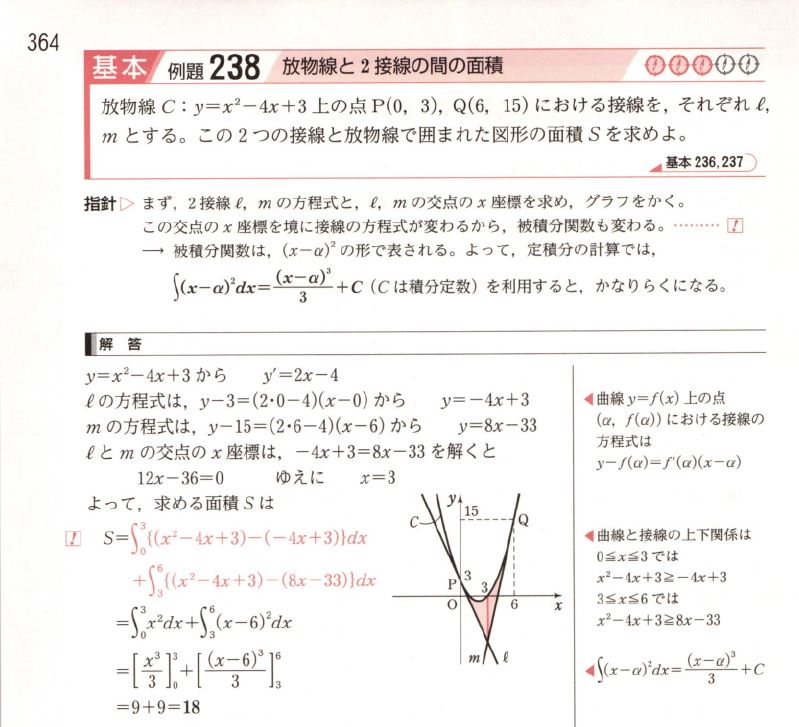
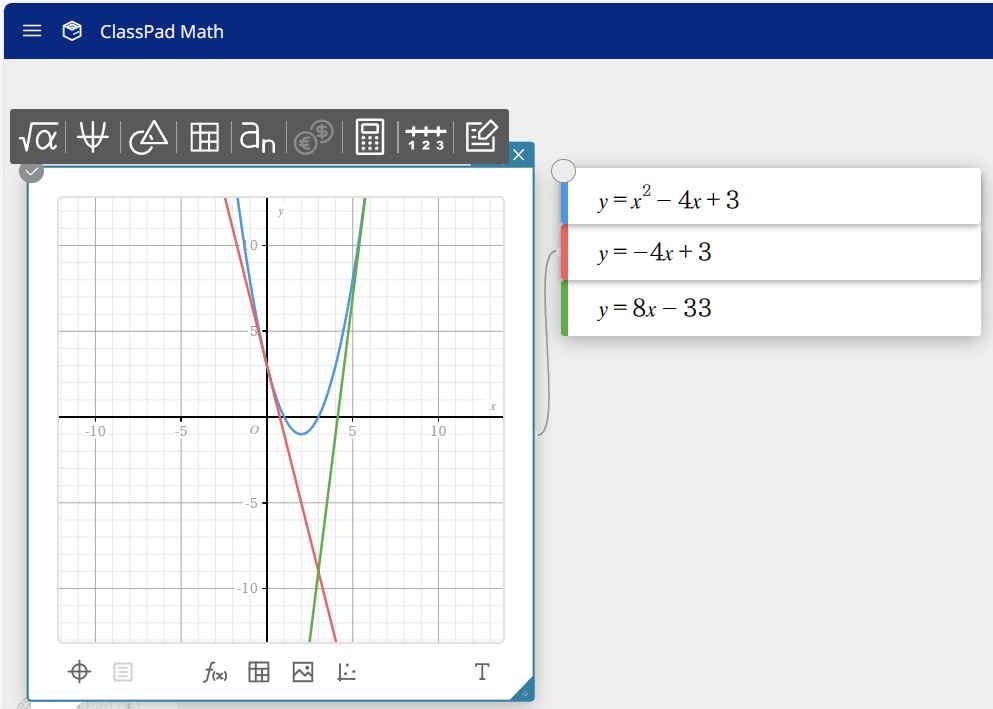
グラフで囲まれた部分は、下記の画像にて示します。(まぁチャート式の解答にも載ってますけどね)
この問題、まずは接線の方程式が求められないと解けない問題です…それは出来ました。
( ホッ と一息 )
でも、個人的には放物線が $ x $ 軸から下にはみ出しているところが気になりました。
「うーむ…この下に凸の部分、マイナスとして扱うのかなぁ…それともプラスのままかなぁ…」
と言った感じです。
でも、これって自分の勉強不足が垣間見えた瞬間です。
解答を見てみて
「あ、そうか…グラフ上で上の方程式から、下の方程式を引いて積分するんだからね」
と、自分の勘違いに気が付いたところです。
いやはや、本当に高校時代は授業中に
「あ、そうか…」
と、納得した時点で、もう終わりにしてましたね。
理解できたと思ったら、実際に問題を解いてみて、正しい答えが導けるかも確かめておかないとね。
これが肝心。
では今日も1日の習慣を始めてます。小さな一歩・挑戦を試みています。
定積分を利用して、複数のグラフに囲まれた部分の面積を求める問題。
高校時代には…
おっと!
まぁ高校時代のことは書くのは止めましょうね。
けっきょく何時もと同じことですから…
(気持ちを切り変えて)
面積を求める問題に関して注意する点は、符号ですよね。
下記の問題でそれを実感しました。

「青チャート式数学II」基本例題248 (改訂版 238) 放物線と2接線の間の面積
放物線 $ C:x^2 -4x +3 $ 上の点 $ P(0,~3),~~Q(6,~15) $ における接線を、それぞれ $ l ,~m $ とする。
この2つの接線と放物線で囲まれた図形の面積 $ S $ を求めよ。
放物線 $ C:x^2 -4x +3 $ 上の点 $ P(0,~3),~~Q(6,~15) $ における接線を、それぞれ $ l ,~m $ とする。
この2つの接線と放物線で囲まれた図形の面積 $ S $ を求めよ。
グラフで囲まれた部分は、下記の画像にて示します。(まぁチャート式の解答にも載ってますけどね)

この問題、まずは接線の方程式が求められないと解けない問題です…それは出来ました。
( ホッ と一息 )
でも、個人的には放物線が $ x $ 軸から下にはみ出しているところが気になりました。
「うーむ…この下に凸の部分、マイナスとして扱うのかなぁ…それともプラスのままかなぁ…」
と言った感じです。
でも、これって自分の勉強不足が垣間見えた瞬間です。
解答を見てみて
「あ、そうか…グラフ上で上の方程式から、下の方程式を引いて積分するんだからね」
と、自分の勘違いに気が付いたところです。
いやはや、本当に高校時代は授業中に
「あ、そうか…」
と、納得した時点で、もう終わりにしてましたね。
理解できたと思ったら、実際に問題を解いてみて、正しい答えが導けるかも確かめておかないとね。
これが肝心。
では今日も1日の習慣を始めてます。小さな一歩・挑戦を試みています。
閲覧(6456)
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |





 前の日記
前の日記



