皆さん こんにちは、時空 解です。

表題にも書きましたが、積分のところで面積を求めるときに見かける公式

$\displaystyle \int (x - \alpha)^2 dx = \frac{ (x- \alpha)^3 }{ 3 } +C$

これって、皆さんは利用する気持ちになるのでしょうか？
私はこういった公式は、高校時代には全く無視！

積極的に利用しようなんて気持ちにはならなかったし、記憶しようとも思いませんでした。
ですからね、この公式が本当に成立しているのか？　なーんて確認、する訳がなかったんです。

でもね…この歳になって気が付いたのですが…計算ミスが多い私です。( ^^;

この公式が利用できれば、確かに楽だしミスも減るんですよね。

例えば昨日もご紹介した問題

「青チャート式数学II」の基本例題２４８ (改訂版 ２３８)

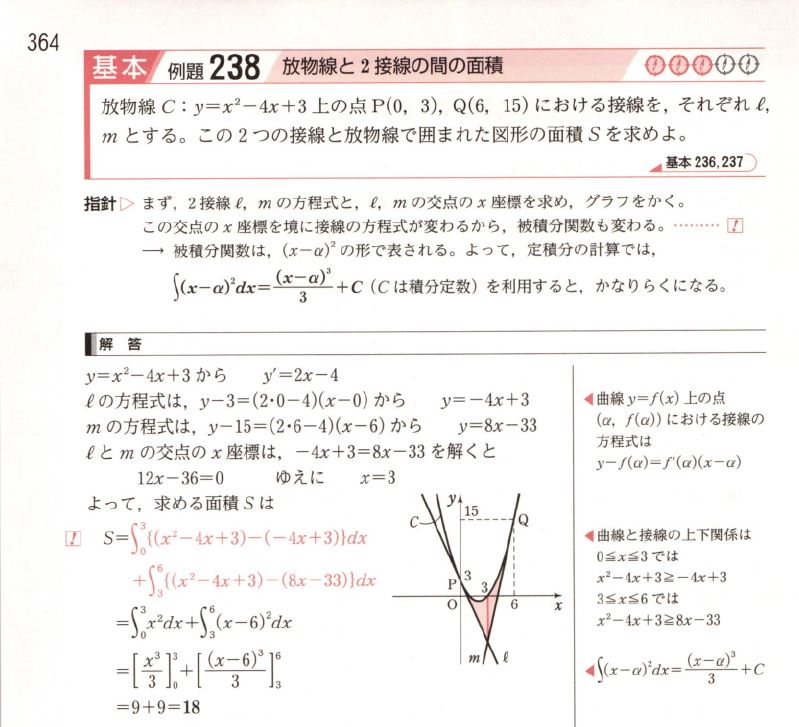
この問題を解くときにも楽になるんです。
先にご紹介した公式がどうして成立しているのか、数研出版さんの解説動画には出てこないのですが…
(公式としての紹介はあります。参照・視聴してみてください)

それで実際に計算、展開してみました。$x$ の範囲は適当に $0$ から $1$ としてね。
そしたら
「おおっ！」
と、ちょっと楽しかった。

皆さんは下記の式変形をたどって見てどう思われますか？

　　　$\displaystyle \int_0^1 (x-\alpha)^2 dx$
　　　$= \displaystyle \int_0^1 (x^2 -2 \alpha x + \alpha^2) dx$
　　　$= \left[ \displaystyle \frac{ x^3}{3} - \alpha x^2 + \alpha^2 x \right]_{0}^{1}$
　　　$= \left[ (\displaystyle \frac{ x^3 - 3 \alpha x^2 + 3 \alpha^2 x }{3}) \right]_{0}^{1}$

これで $\displaystyle \frac{ (x - \alpha)^3 }{ 3 }$ が見えますよね？！　　積分定数 $C$ が $\displaystyle \frac{ \alpha^3 }{ 3 }$ てとこですね。

数学がちょっと楽しくなった今日です。
この公式、これからは利用しようっと　

では今日も１日の習慣を始めてます。小さな一歩・挑戦を試みています。