皆さん こんにちは、時空 解です。

表題の通り、今日は 第422回２級2次、問題６ (必須問題) に付いて書いてみたいと思います。
(問題と解答は右画像参照のこと)

この問題、まず設問 (1) の問題文には
　　　$ \cos A = \cos B = \displaystyle \frac{ 1 }{ 2 } $
とあります。

これって、
$ \cos \theta = \displaystyle \frac{ 1 }{ 2 } $
と問われたら、$ \theta $ の取る角度がピンとくる方も多いのではないでしょうか？

　　　$ \theta = 60^\circ $ or $ 300^\circ $

ですよね。問題は三角形の一つの角ですから $ 60^\circ $ とわかります。

結果として、設問 (1) の $ \triangle ABC $ は正三角形だと想像できれば、

　　　$ \sin C = \sin60^\circ = \displaystyle \frac{ \sqrt{ 3 } }{ 2 } $

と、すぐにわかります。記述する内容はほとんどありません。

ですから問題文にも
「答えだけを書いてください」
と書かれているのだと思います。

それから設問の (2) と (3) ですが…
これも使われている文字で混乱する気がします。

問題文で問われている $ \triangle ABC $ を描いて文字を余弦定理、正弦定理の公式に対応させてやれば見えてきますよね。

CASIO さんの「ClassPad Math」を利用して図示してみました。

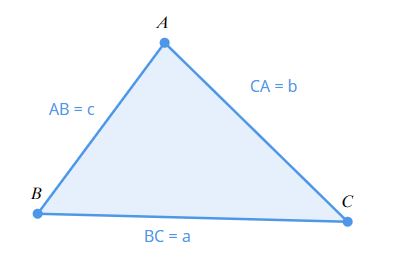
この図をみながら問題文を下記のように読みかえると、余弦定理の公式を２次方程式として $ CA = b $ の辺の長さを導けます。
 
これで設問 (2) は余弦定理より
　　　$ a^2 = b^2 + c^2 -2bc \cos{A} $
という式を得ます。わかっている値を代入してやると
　　　$ (b+1)^2 = b^2 + 7^2 -2 \cdot b \cdot 7 \cdot \displaystyle \frac{ 4 }{ 7 } $
となります。

あとは $ b $ を計算するだけですよね。

おっと、もうこんな時間だ。朝の身支度しないと…( ^^;
今日はこの辺で。

では今日も１日の習慣を始めてます。小さな一歩・挑戦を試みています。