時空 解 さんの日記
2024
4月
16
(火)
09:31
本文
皆さん こんにちは、時空 解です。
表題の通り、今日は 第422回2級2次、問題7 (必須問題) に付いて書いてみたいと思います。
(問題と解答は右画像参照のこと)

これは定番の問題ですよね。
まずは問題で与えられている3次方程式を ClassPad Math を使ってグラフ化してみましょう。
そうすると問題の意図もわかりやすくなります。
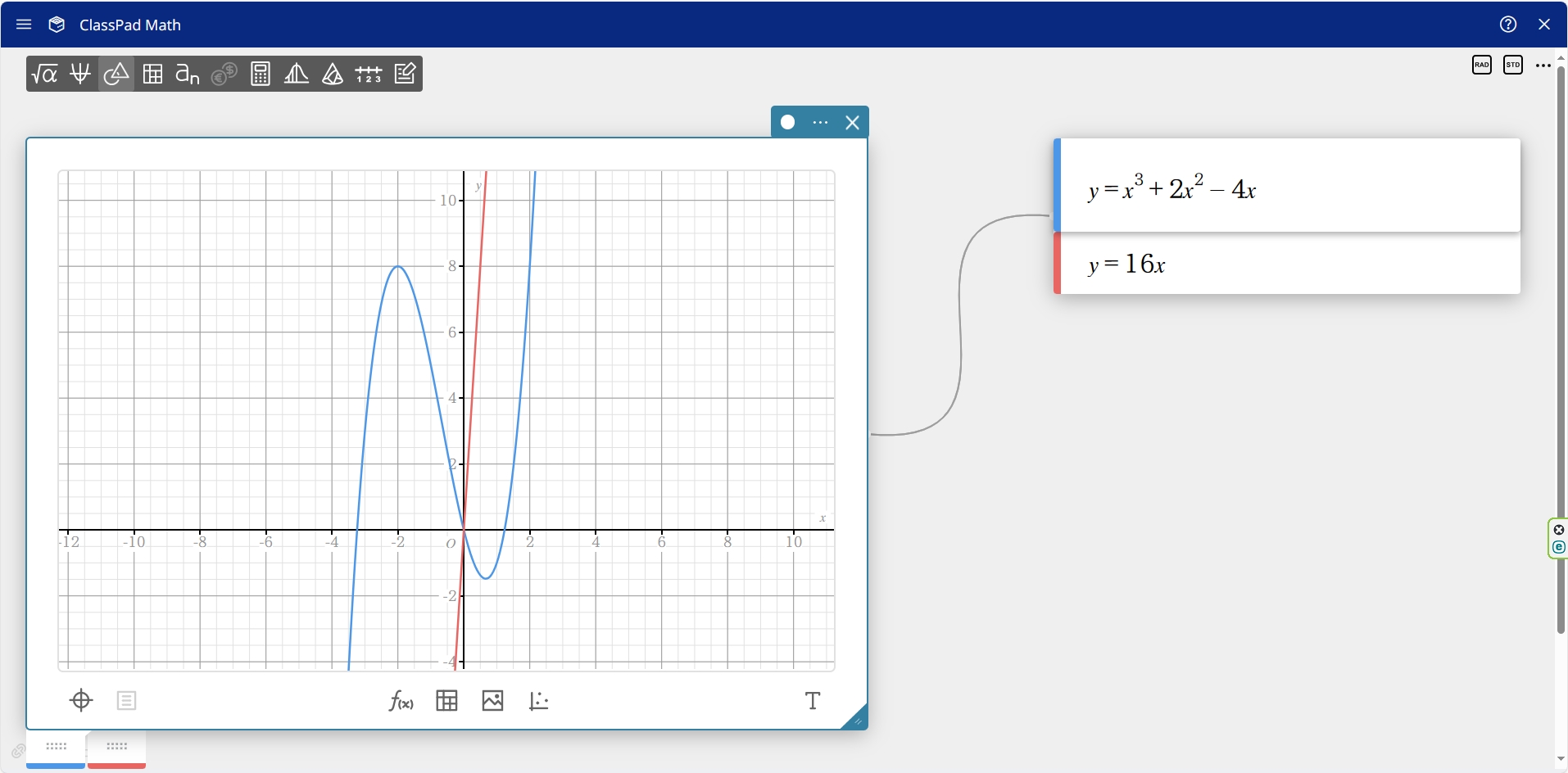
3次方程式の極値と言うのは、接線の傾きが $ 0 $ になるところですよね。
模範解答には
$ f'(x) = 0 $
と言う記述はありませんけどね。
…個人的に、ここがちょっと腑に落ちませんが… ( ^^;
まぁ増減表の中にちゃんと $ 0 $ が載っているので良しとしましょう。
この設問 (1) に付いては模範解答を参考にして、記述できるようにしておけば OK ですね。
設問 (2) に付いては、$ y = 16x $ に平行な接線と言うことなので、点 $ ( a,~ f(a)~) $ の接線の傾きが $ 16 $ と言うことですよね。
それさえ分かれば後は与式 $ f(x) = x^3 +2x^2 -4x $ の微分を使って
$ f'(a) = 3a^2 +4a -4 = 16 $
を解くだけですよね。
この問題は検定中に
「解けた」
と思った問題でした。でもね…結果は、$ 1 $ 点中の $ 0.8 $ 点だったんです。
うーむ…何を減点されたのだろう…。
設問 (1) に付いて "シンプルな記述" じゃなかったからかな? ( ^^;
問うているのは
・増減表を調べよ
・極大値、極小値とその時の $ x $ の値を求めよ
ですからね。
「極値は $ f'(x) = 9 $ のところに現われるから…」
なんて余分な解説なんでしょうね…_| ̄|○
では今日も1日の習慣を始めてます。小さな一歩・挑戦を試みています。
表題の通り、今日は 第422回2級2次、問題7 (必須問題) に付いて書いてみたいと思います。
(問題と解答は右画像参照のこと)

これは定番の問題ですよね。
まずは問題で与えられている3次方程式を ClassPad Math を使ってグラフ化してみましょう。
そうすると問題の意図もわかりやすくなります。

3次方程式の極値と言うのは、接線の傾きが $ 0 $ になるところですよね。
模範解答には
$ f'(x) = 0 $
と言う記述はありませんけどね。
…個人的に、ここがちょっと腑に落ちませんが… ( ^^;
まぁ増減表の中にちゃんと $ 0 $ が載っているので良しとしましょう。
この設問 (1) に付いては模範解答を参考にして、記述できるようにしておけば OK ですね。
設問 (2) に付いては、$ y = 16x $ に平行な接線と言うことなので、点 $ ( a,~ f(a)~) $ の接線の傾きが $ 16 $ と言うことですよね。
それさえ分かれば後は与式 $ f(x) = x^3 +2x^2 -4x $ の微分を使って
$ f'(a) = 3a^2 +4a -4 = 16 $
を解くだけですよね。
この問題は検定中に
「解けた」
と思った問題でした。でもね…結果は、$ 1 $ 点中の $ 0.8 $ 点だったんです。
うーむ…何を減点されたのだろう…。
設問 (1) に付いて "シンプルな記述" じゃなかったからかな? ( ^^;
問うているのは
・増減表を調べよ
・極大値、極小値とその時の $ x $ の値を求めよ
ですからね。
「極値は $ f'(x) = 9 $ のところに現われるから…」
なんて余分な解説なんでしょうね…_| ̄|○
では今日も1日の習慣を始めてます。小さな一歩・挑戦を試みています。
閲覧(7153)
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |





 前の日記
前の日記



