時空 解 さんの日記
2024
4月
19
(金)
09:41
本文
皆さん こんにちは、時空 解です。
表題の通り、今日は ClassPad Math を利用して、青チャート式数学の問題を考察してみました。
ClassPad Math は考えるときの役に立つんですよね。
まぁ ClassPad Math は ICT学習アプリ の1つですがね、役に立つのは当然のことなんです。
でも、実際に使ってみないと、その便利さは実感できません。積極的に使って行くのもいいかと思います。

と言うことで今日は実際に
「青チャート式数学II 第7章 積分法」基本例題255 を考察してみました。
この問題の解法はチャート式の解答を参照して頂くとして…
(判別式 $ D $ をどう最小値として考えるかと $ \displaystyle \frac{ 1 }{ 6 } $ 公式の利用がポイント)
問題を分かりやすくするために ClassPad Math で出来ることをやってみました。それが下画像です。
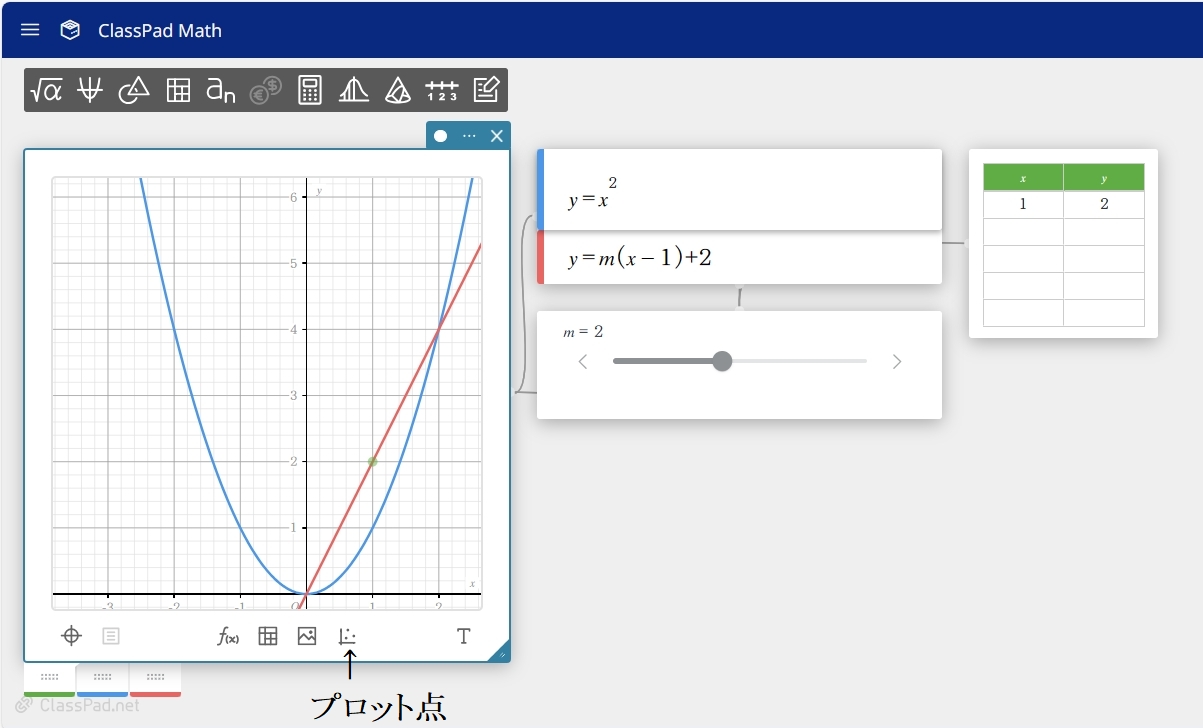
素晴らしいです、操作方法は直感で手探りしたら、簡単に描けたんですから。
ちょっと迷ったのは
・点 $ (1,~2) $ をグラフに描くにはどうしたらよいか?
と言うことのみです。
でもこれも "プロット点" さえ分かれば直ぐに描けます。
皆さんも、数学の学習時に ClassPad Math を積極的に使ってみてはいかがてしょうか?
では今日も1日の習慣を始めてます。小さな一歩・挑戦を試みています。
表題の通り、今日は ClassPad Math を利用して、青チャート式数学の問題を考察してみました。
ClassPad Math は考えるときの役に立つんですよね。
まぁ ClassPad Math は ICT学習アプリ の1つですがね、役に立つのは当然のことなんです。
でも、実際に使ってみないと、その便利さは実感できません。積極的に使って行くのもいいかと思います。

と言うことで今日は実際に
「青チャート式数学II 第7章 積分法」基本例題255 を考察してみました。
「青チャート式数学II 第7章 積分法」基本例題255 (改訂版244)
点 $ (1,~2) $ を通る直線と放物線 $ y = x^2 $ で囲まれる図形の面積を $ S $ とする。
$ S $ の最小値を求めよ。
点 $ (1,~2) $ を通る直線と放物線 $ y = x^2 $ で囲まれる図形の面積を $ S $ とする。
$ S $ の最小値を求めよ。
この問題の解法はチャート式の解答を参照して頂くとして…
(判別式 $ D $ をどう最小値として考えるかと $ \displaystyle \frac{ 1 }{ 6 } $ 公式の利用がポイント)
問題を分かりやすくするために ClassPad Math で出来ることをやってみました。それが下画像です。

素晴らしいです、操作方法は直感で手探りしたら、簡単に描けたんですから。
ちょっと迷ったのは
・点 $ (1,~2) $ をグラフに描くにはどうしたらよいか?
と言うことのみです。
でもこれも "プロット点" さえ分かれば直ぐに描けます。
皆さんも、数学の学習時に ClassPad Math を積極的に使ってみてはいかがてしょうか?
では今日も1日の習慣を始めてます。小さな一歩・挑戦を試みています。
閲覧(2449)
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |





 前の日記
前の日記



