皆さん こんにちは、時空 解です。

「青チャート式数学II」の "新課程" の方にしかない載ってない問題 (改訂版にはない) を解いていました。

おっと！

"解いていた" のではなくて、解説動画を視聴して、内容を理解していたんですけどね。( ^^;
とても自分独りでは解けない問題だろうなぁと思います。

その問題がこれ (右画像参照)

まぁ時間を掛ければ答えを導くことはできたかも知れません。
解答に載っている【参考】のようにね。

でも数学検定などで出題されたとしたら…やっぱり数式の変形ミスをする可能性が高いです。

と言うことで、この問題のポイントは
如何にして６分の１公式に持って行くか
と言うことになりますが。

うーむ…解答に載っているように下の図から、$ S_2 $ をどうやって６分の１公式に絡めて求めるか、です。

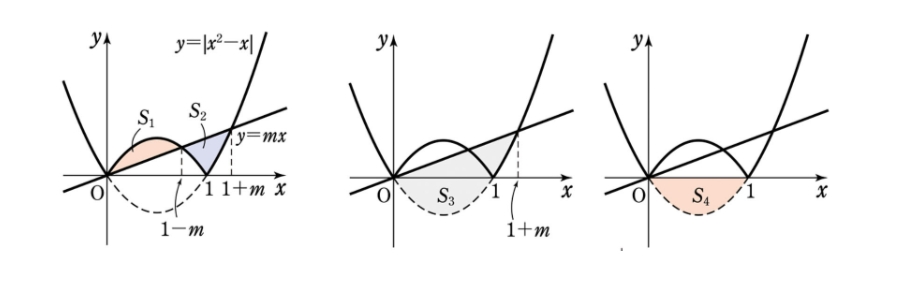
私には思いつかない。＿|￣|○

$ S_2 $ を求めるために、わざわざ $ S_1 $ を足し込む発想…ここに驚きました、私…。

学生時代にはこの手の発想が得意だと思っていた自分ですが…今ではできない？
それとも、実は学生時代でもできなかった？

まぁとにかく今は出来なかった、と言う事実だけが明確ですね…とほほ。

では今日も１日の習慣を始めてます。小さな一歩・挑戦を試みています。