皆さん こんにちは、時空 解です。

さて、今日は必須問題に進みます。

第４２７回 数学検定２級２次　問題６ (必須) 



この問題は２次方程式の判別式を使って解く問題でしょう。

まずは
　　　$ y = \displaystyle \frac{1}{2} x^2 + (k-2)x + k^2 -5k -6 $
の判別式は
　　　$ D = -k^2 + 6k +16 $

ですから、これが２つの実数解を持つためには $ D \gt 0 $ であればいいですよね。

　　　$ k^2 - 6k -16 \lt 0 $
　　　$ (k-8)(k+2) \lt 0 $
　　　　　　　　　　　　　$ \therefore -2 \lt k \lt 8 $　　…(a)

つぎに
　　　$ y = -2x^2 + 4(k+3)x - \displaystyle \frac{5}{2} k^2 -11k -6 $
の判別式は
　　　$ D' = -k^2 +2k +24 $

ですから、同様に $ D' \gt 0 $

　　　$ k^2 -2k -24 \lt 0 $
　　　$ (k-6)(k+4) \lt 0 $
　　　　　　　　　　　　　$ \therefore -4 \lt k \lt 6 $　　…(b)

(a), (b) ２つを同時に満たす $ k $ が設問 (1) の求めている答えなので

　　　設問 (1) の答え： $ -2 \lt k \lt 6 $


この設問 (1) の答えが出せれば、設問 (2) もすぐに答えは出てきます。



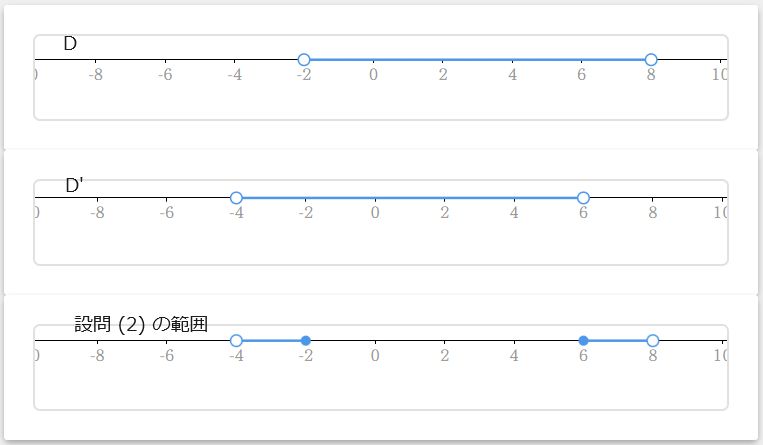
気を付けなくてはいけないのが、範囲の区切りのところ。
含むか含まないかをちゃんと不等号で記述しないとね。

　　　設問 (2) の答え： $ -4 \lt k \leqq -2 $、$ 6 \leqq k \lt 8 $

数直線をちゃんと書けば、間違えずに答えを書くことが出来ると思います。

では今日も休日を始めています。休日の充実こそ、人生の充実です。