皆さん こんにちは、時空 解です。

さて、今日で第４２７回の数学検定２級２次の問題も最後となります。

第４２７回 数学検定２級２次　問題７ (必須)



この問題は微分が入っているので取っつき難いところがありますが、落ち着いて見れば何のことはない、恒等式の問題ですよね。

まずは $ f_{(x)} $ を微分してみましょう。

　　　$ f'_{(x)} = 3ax^2 +2bx +c $
　　　$ x f'_{(x)} = 3ax^3 +2bx^2 +cx $
ですから
　　　$ f_{(x)} + x f'_{(x)} = 4ax^3 +3bx^2 +2cx +d $

ですよね。これが $ -4x^3 +18x^2 +14 $ だと問題文では言っていますので

　　　$ -4x^3 +18x^2 +14 = 4ax^3 +3bx^2 +2cx +d $

とすることができて、恒等式の性質より

　　　$ -4 = 4a $
　　　$ 18 = 3b $
　　　$ 0 = 2c $
　　　$ 14 = d $

となります。これを解くと設問 (1) の答えが出てきます。

　　　設問 (1) の答え：$ (a,~b,~c,~d) = (-1,~6,~0,~14) $

これより $ f_{(x)} = -x^3 +6x^2 +14 $ であることが分かります。
設問 (2) はこの $ f_{(x)} $ の増減と極値と、そのときの $ x $ 値を求める問題ですが、これは定番の問題ですよね。

　　　$ f'_{(x)} = -3x^2 +12x $　より


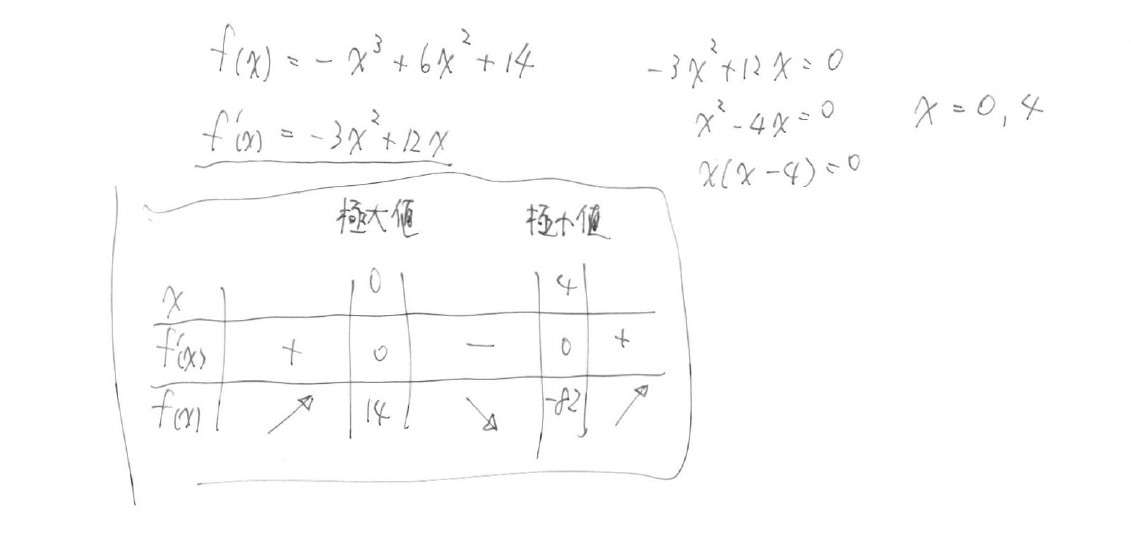
この画像は、数学検定２級２次を受検中に、問題用紙の方に記述したものです。
２次検定が始まって、まずは必須の問題２つを解いておいたんです。

解答用紙への記述は最後に…と、この時は考えていました。でもね…

最後の最後、２次検定が終了する直前になって解答用紙に上記を書き写そうとしたのですが…時間切れになってしまいました。

四角で括ってある "増減表" のみを記述するに終わり…何点貰えるのかなぁ…＿|￣|○

では今日も１日の習慣を始めてます。小さな一歩・挑戦を試みています。