皆さん こんにちは、時空 解です。

昨日は折に触れて、「青チャート式数学Ｂ」の P464,465 と格闘していました。

ですが、今日の朝に次のページをめくってくたら…　！
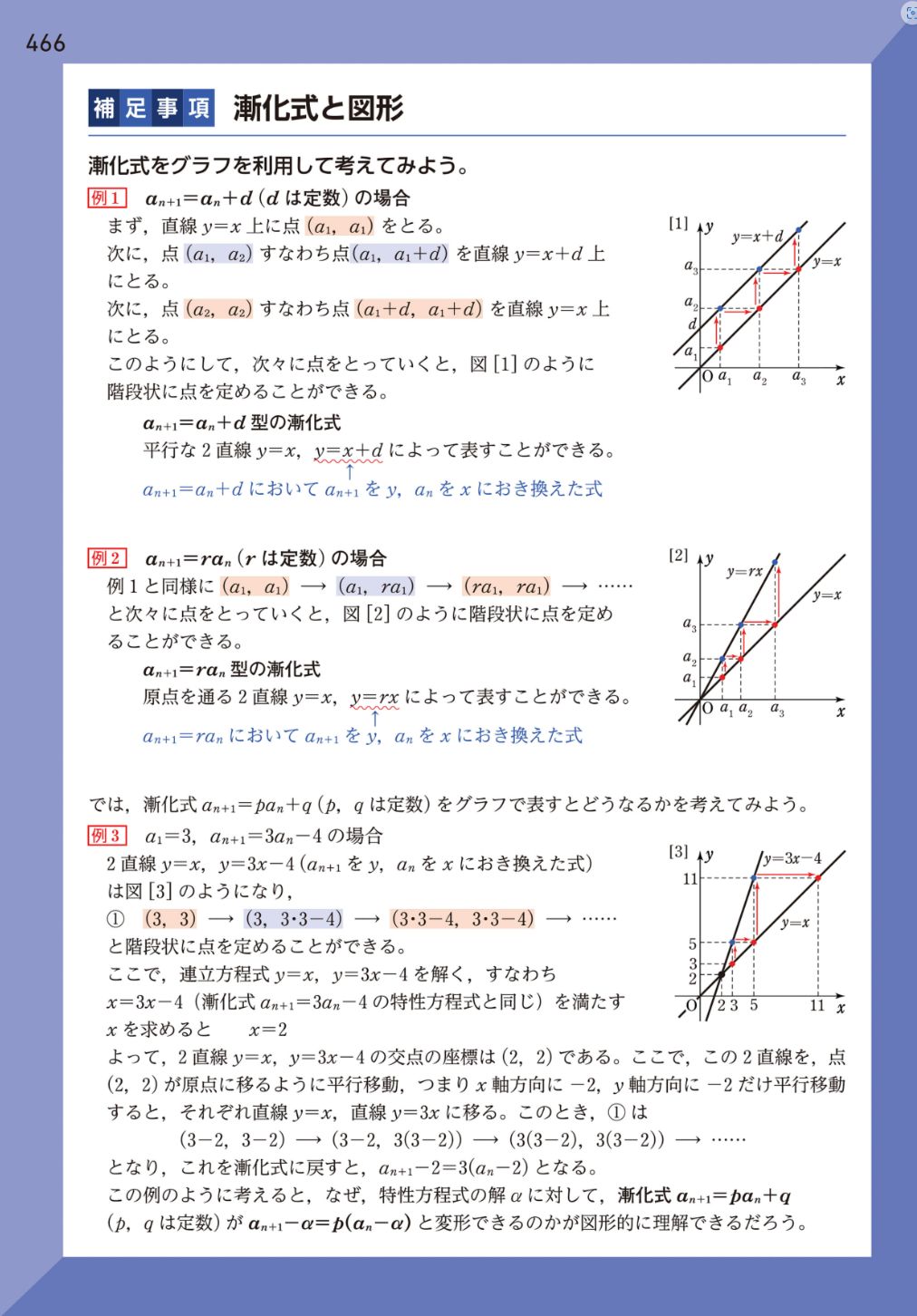
・補足事項　漸化式と図形　(右画像参照)

なんと、
　　　$ a_{n+1} = \alpha $、$ a_n = \alpha $
つまり
　　　$ a_{n+1} = a_n $
となるような $ \alpha $ を置く理由がグラフ図形的に解説されていました。

なるほどぉ…！

２つの直線の方程式。
\begin{equation}
    \begin{cases}
        y = x \\
        y = px + q
    \end{cases}
\end{equation}

この直線の交点が、特性方程式の $ \alpha $ の値だったんですね。
　　　$ y = x $
上記の直線方程式が、すなわち
　　　$ a_{n+1} = a_n = \alpha $
を表している部分ですね。

これ以上に納得のできる解説はないのではないでしょうか？

２つの直線の交点がグラフの原点にくれば、それで等差数列のグラフの形になります。

昨日は同じページばかりを見て考えていた私です。( ^^;
次のページを開いて、シッカリと目を通していたら、これだけの解説に巡り会えていたのに…＿|￣|○

こういうところがバカですよね。次のページを開きもしない。開いても流し読みをして事の重大さに気が付かない…

学生時代は勉強がやりたくなくて "勉強している振り" ばかりしてましたからね…この癖が身に付いているように思う今日このごろです…。

では今日も充実した日を過ごす予定です。
充実した日々には楽しむ日もあっていいよね。