時空 解 さんの日記
2017
2月
1
(水)
22:15
前の日記
本文
皆さんこんにちは。時空 解です。
先日チョットふれましたが、数学検定の３級となると難しい問題が出て来ます。３級用のテキスト「実用数学技能検定 要点整理 ３級」の 24ページ の発展問題もその一つです。
先日チョットふれましたが、数学検定の３級となると難しい問題が出て来ます。３級用のテキスト「実用数学技能検定 要点整理 ３級」の 24ページ の発展問題もその一つです。
始めはチンプンカンプンでした。
でも数字の位取り表記の意味を考えれば分かってきます。これは足し算・引き算の時に出てくる「くり上がり」・「くり下がり」にも関連があります。もしかしたら算数の中で小学生が一番初めに突き当たる壁、と言ってもいいかも知れません。
引き算をしている時に出てくる "くり下がり"
「どうして２つ上から借りてくるときに、始めは 9 で最後は 10 なの？」
と言うやつですね。
引き算をしている時に出てくる "くり下がり"
「どうして２つ上から借りてくるときに、始めは 9 で最後は 10 なの？」
と言うやつですね。
では 24ページの発展問題を下記に書いてみましょう。
| 問題 | １から９の数字が１つずつ書かれた９個の球を袋に入れ、よくかき混ぜてから同時に３個の球を取り出します。取り出した球に書かれている数を大きい方から順に a, b, c として、a, b, c を使ってできる３けたの正の整数のうち、最大の数から最小の数をひいた差を調べます。 たとえば、a = 7, b = 4, c = 3 のときは、 347, 374, 437, 473, 734, 743 の６通りの数ができ、最大の数から最小の数をひいた差は、 743 - 347 = 396 です。このとき、次の問いに答えなさい。 (1) ３個の球を取り出してできる最大の数から最小の数をひいた差は 99 の倍数になることを a, b, c を使って説明しなさい。 (2) 最大の数から最小の数をひいた差が 297 になるような a, b, c の組は全部で何通りありますか。 |
| 答え | (1) ３個の整数 a, b, c ( a>b>c ) を使ってできる最大、最小の数はそれぞれ、100a + 10b + c, 100c +10b + a と表される。 このとき、求める差は、 100a + 10b + c - (100c + 10b + a) = 99a - 99c = 99(a - c) a - c は整数だから、99(a - c) は 99 の倍数である。 したがって、３個の球を取り出してできる最大の数から最小の数をひいた差は 99 の倍数になる。 (2) ( …この解答解説はまたいずれ… ) |
上記の (1) の問題は、数字の位取り表記の意味を理解しているかを問う問題だと私は思いました。
みなさん、1000 - 1 はいくつでしょう？ 999 ですよね。
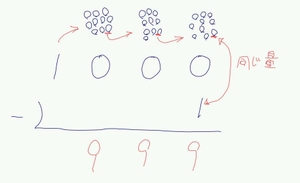これを筆算を使って書くと右図のようなイメージを私は思い浮かべます。ひきたい数字は一の位の 1 ( これを ミカン一個としましょうか ) ですから、千の位からこの 1 をひくためには、百の位、十の位、そして一の位まで、十のまとまりを順に分解して行く必要があります。これがくり下がりですね。
十進法の位取り表記と言うのは、10個の塊が出来るたびに位を一つ上げて書く書き方です。
数字を書き並べる時に、数字を書く場所( 位 ) に重みを持たせた訳です。ゼロの発見で可能になった数量の表記ですよね。
数字を書き並べる時に、数字を書く場所( 位 ) に重みを持たせた訳です。ゼロの発見で可能になった数量の表記ですよね。
ミカンがたくさんあった場合その個数を数える方法で位取り表記法を考えてみましょう。
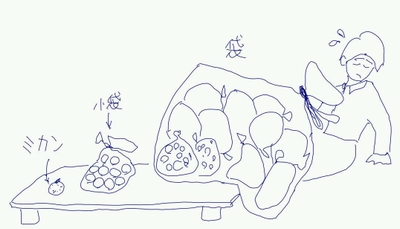位取り表記がまだ発明されていない昔では、たくさんのミカンをどのように数字表記していたかと言うと、９個まではそのまま数字を対応させましたが、1０個集まったら一つの小袋に入れましょう、という具合にやりました。これでミカンが１０個ある事を昔は "１小袋" と書いたと言う事です。１１個ならば "１小袋と１個" と表記されるわけです。では１００個のミカンは？と言うと１０小袋。でも先ほどの「１０個集まったら一つ…」と言う法則に従えば、小袋より大きい袋に入れて "１袋" とでも表記する事になります。 "小袋" が10個入った "袋" ですね。では１０００はと言うと "１袋" が１０個入るもっと大きい袋となります。１大袋とでも表記するのが妥当でしょうか…。
こうなるとミカンが２７２３個の場合、昔の表記では "２大袋７袋２小袋と３個" となります。
さて、ミカンの数を表記するなら袋みたいな単位を使うのもいいですが、人数を表すとなると不適切ですよね。新しい表現・単位を考えたくなります。それにミカンであっても、１００００個、１０００００個と言う大きい量だと、大袋以上に大きい袋を表す言葉を作って行かなくてはなりません。
こうしてみると位取り表記と言うのは便利な物です。
数字文字をただ並べるだけで、最後に "個" とか "人" と書き足すだけで済みます。
( 位取り表記が発明されるまでの苦労は左に示す「異端の数ゼロ」に出て来ます )
数字文字をただ並べるだけで、最後に "個" とか "人" と書き足すだけで済みます。
( 位取り表記が発明されるまでの苦労は左に示す「異端の数ゼロ」に出て来ます )
現代では位取り表記で、十進法が採用されています。
十進法とはミカンが１０個集まったら小袋に…と言うように、１０集まったら一つ位を上げて書く、と言う表記です。五進法と言うとミカンが５個集まったら小袋に…と言う事です。１小袋に１０個入れるのではなく、５個入れると決めるのですよね。そして使う数字記号は 0, 1, 2, 3, 4 の４つ。
これで十進法で言うミカン７個は、五進法ではどう表記されるかと言うと…１２個と表記されると分かりますよね？ "１小袋と２個" なのです。
十進法とはミカンが１０個集まったら小袋に…と言うように、１０集まったら一つ位を上げて書く、と言う表記です。五進法と言うとミカンが５個集まったら小袋に…と言う事です。１小袋に１０個入れるのではなく、５個入れると決めるのですよね。そして使う数字記号は 0, 1, 2, 3, 4 の４つ。
これで十進法で言うミカン７個は、五進法ではどう表記されるかと言うと…１２個と表記されると分かりますよね？ "１小袋と２個" なのです。
さてこのミカンの話を前提に発展問題 (1) を考えると、問題文は a を袋、b を小袋、そして c は個数に対応させられます。しかも一番大きい数字を a, 真ん中を b, そして一番小さいのを c とする、と指示があります。取り出した球が例えば 1 と 8 と 3 だったとすると "a = 8, b = 3, c = 1 のように対応させろ" と言う指示です。
ここで a = 8 と言うのはミカン風に考えると "８袋" となります。"１袋" の中には小袋が１０、つまり 8 × "１０小袋" です。"１小袋" には１０個のミカンが入っているので、8 × 10 × 10 でミカンの個数が計算できます。ここまでくれば 100a の意味、分かりますよね。３小袋は 3 × 10 なので 10b 。c はそのままの c となります。
このことから発展問題の(1) の答えの中の式、
100a + 10b + c - (100c + 10b + a) = 99a - 99c = 99(a - c)
この意味が良く分かってくると思います。
一の位である c はそのまま c。十の位は b × 10 = 10b。百の位は a × 100 = 100a と計算して、個数と位の対応が一致している事が感じてもらえると思います。
ここで a = 8 と言うのはミカン風に考えると "８袋" となります。"１袋" の中には小袋が１０、つまり 8 × "１０小袋" です。"１小袋" には１０個のミカンが入っているので、8 × 10 × 10 でミカンの個数が計算できます。ここまでくれば 100a の意味、分かりますよね。３小袋は 3 × 10 なので 10b 。c はそのままの c となります。
このことから発展問題の(1) の答えの中の式、
100a + 10b + c - (100c + 10b + a) = 99a - 99c = 99(a - c)
この意味が良く分かってくると思います。
一の位である c はそのまま c。十の位は b × 10 = 10b。百の位は a × 100 = 100a と計算して、個数と位の対応が一致している事が感じてもらえると思います。
これでうまく説明出来ているかは分かりませんが、これが私なりのこの問題の解釈です。
参考になれば嬉しいですね。
参考になれば嬉しいですね。
(2) に付いてはまた明日、出来れば書きたいと思います。…でも結構時間が掛かりそうなので、あまり期待しないでね。
では今日はこの辺で。
千里の道も一歩から…。
(ポチッと右のバナーをクリックしてね）
「良い習慣化計画」
朝は七時に起きます。
夜は１１時に寝ます。
数学、物理の勉強をします。
ブログを毎日更新します。
勉強会の動画は YouTube チャンネル でご覧になれます。
千里の道も一歩から…。
(ポチッと右のバナーをクリックしてね）
「良い習慣化計画」
朝は七時に起きます。
夜は１１時に寝ます。
数学、物理の勉強をします。
ブログを毎日更新します。
勉強会の動画は YouTube チャンネル でご覧になれます。
閲覧(5559)
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |
メインメニュー
