時空 解 さんの日記
2025
2月
16
(日)
20:03
本文
皆さん こんにちは、時空 解です。
「青チャート式数学B」の第1章:数列、3いろいろな数列
のところで、重要例題32があります。これは格子問題なんですが。
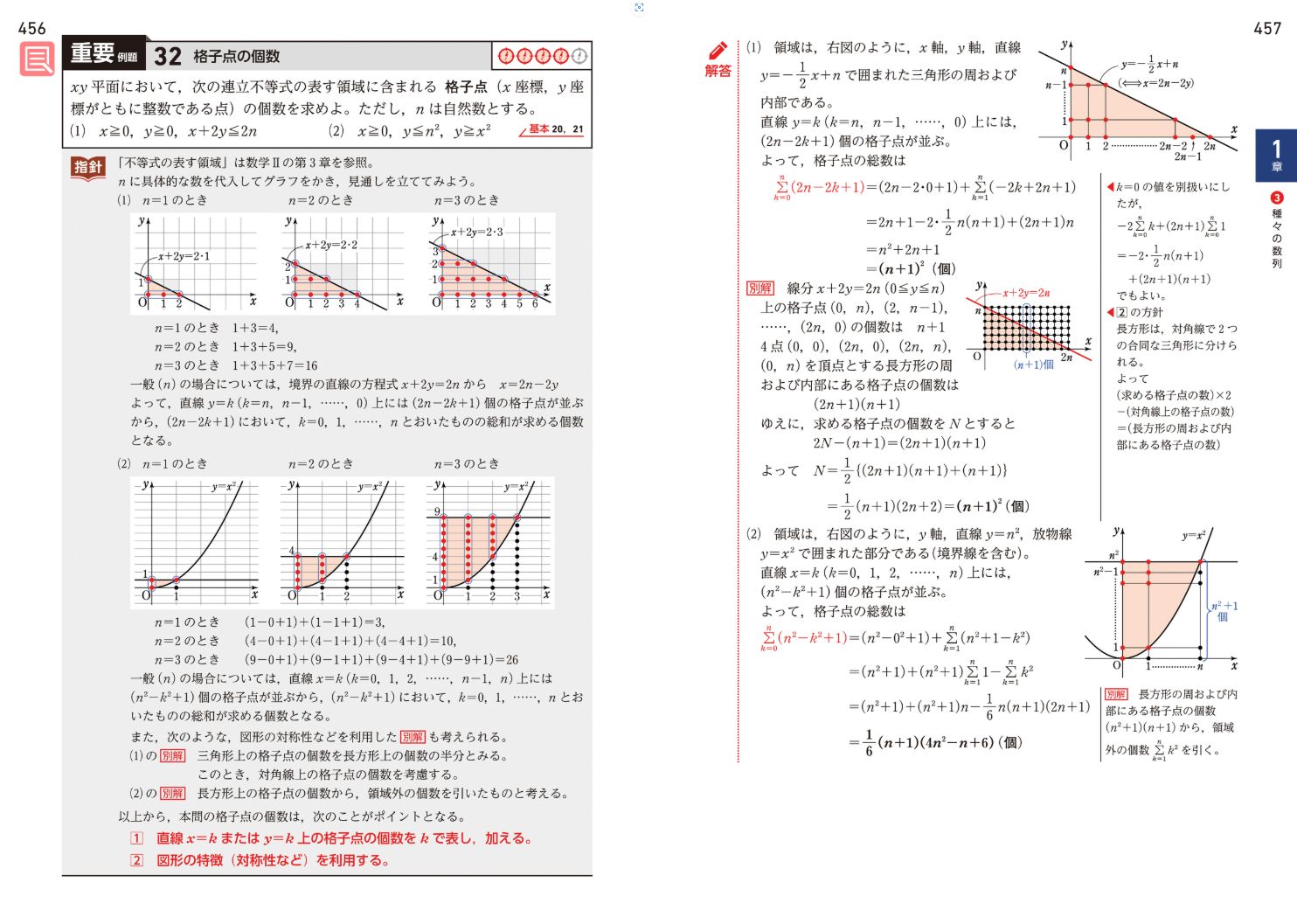
この問題には幾度となく壁にぶつかってきました。
例えば過去に下記のブログを投稿しています。
・これが高校の数学なんですね…ピックの定理
まぁこの重要例題32はピックの定理を使って解く問題ではありませんが、延長線上にはピックの定理が見え隠れする問題と言うことです。
とにかくこの問題解法がやっと理解できた次第なんです。恥ずかしながら…( ^^;
この問題のポイントは下記の三点でしょう。
・格子の数をどうやって数列に結びつけるか?
・格子の数は座標の $ 0 $ のところにもある。それを数列でとう処理するか?
・シグマの公式を使うときに $ k = 0 $ をどう処理するか?
過去には
「何だこの問題、数学らしくない問題だなぁ…」
とぼやいていた私ですが…。
上記のようにポイントを整理してみると、良い問題だなぁと想ったりもしました。
…と言うか、やっとちゃんと理解できるようになった…と言うことです。
やっと解説動画の言っていることが分かるようになったんですよね。
直接公式を使えない状況でも、それを上手に処理することも数学のうち。
例えば "三角形の面積を求めたい" と言うのならばその公式を使えばいいことで…。
でも、もう高校の数学Bともなると問題が数学になるんですね。
…まぁ簡単に言えば "応用が必要" と言うことですが。( ^^;
でもやっぱりこの重要例題32は、数列を上手に利用できる頭がないと解けない問題ですよね。
シグマの公式は $ k = 0 $ とか $ k = 1 $ とか、$ n $ とか $ n+1 $ とか…
重要例題32は難しいけど、解けるようにしないと数学を利用できる頭には成れないでしょう。
では今日も1日の習慣を始めてます。小さな一歩・挑戦を試みています。
「青チャート式数学B」の第1章:数列、3いろいろな数列
のところで、重要例題32があります。これは格子問題なんですが。

この問題には幾度となく壁にぶつかってきました。
例えば過去に下記のブログを投稿しています。
・これが高校の数学なんですね…ピックの定理
まぁこの重要例題32はピックの定理を使って解く問題ではありませんが、延長線上にはピックの定理が見え隠れする問題と言うことです。
とにかくこの問題解法がやっと理解できた次第なんです。恥ずかしながら…( ^^;
この問題のポイントは下記の三点でしょう。
・格子の数をどうやって数列に結びつけるか?
・格子の数は座標の $ 0 $ のところにもある。それを数列でとう処理するか?
・シグマの公式を使うときに $ k = 0 $ をどう処理するか?
過去には
「何だこの問題、数学らしくない問題だなぁ…」
とぼやいていた私ですが…。
上記のようにポイントを整理してみると、良い問題だなぁと想ったりもしました。
…と言うか、やっとちゃんと理解できるようになった…と言うことです。
やっと解説動画の言っていることが分かるようになったんですよね。
直接公式を使えない状況でも、それを上手に処理することも数学のうち。
例えば "三角形の面積を求めたい" と言うのならばその公式を使えばいいことで…。
でも、もう高校の数学Bともなると問題が数学になるんですね。
…まぁ簡単に言えば "応用が必要" と言うことですが。( ^^;
でもやっぱりこの重要例題32は、数列を上手に利用できる頭がないと解けない問題ですよね。
シグマの公式は $ k = 0 $ とか $ k = 1 $ とか、$ n $ とか $ n+1 $ とか…
重要例題32は難しいけど、解けるようにしないと数学を利用できる頭には成れないでしょう。
では今日も1日の習慣を始めてます。小さな一歩・挑戦を試みています。
閲覧(362)
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |





 前の日記
前の日記



