皆さん こんにちは、時空 解です。

今日は朝、ギョッとした問題に出くわしました。
「受かる！数学検定_2級」の中に出てくる問題なんですけどね。

それがこちら
 
答は右画像に示しておきました。

この問題、ポイントとなるところは
「解がすべての実数のとき」
と言う点ですかね。

等式の場合、例えば $ x^2 -2kx +3k +4 = 0 $ とかだとね、よく出題されるパターンとしては
「実数解が２つのとき」
とか
「重解のとき」
とか、もしくは
「解が無いとき」
と言う問題もありますよね。

こんな、等式の問題に頭が慣れているところで、
「解がすべての実数のとき」
と、突然に問われてたのです、今日の朝にね。

ちょっと混乱しました。
「判別式で、解が無いときは $ D \lt 0 $ だからなぁ…」
と連想した私には "解がすべての実数のとき" なんて問われてるチンプンカンプンだった訳です。

でも、グラフを描いてみて落ち着いて来ました。

問題の題意「解がすべての実数のとき」と言うのは、双曲線グラフが全て $ x $ 軸よりも上側。つまり $ y \gt 0 $ ですよね。


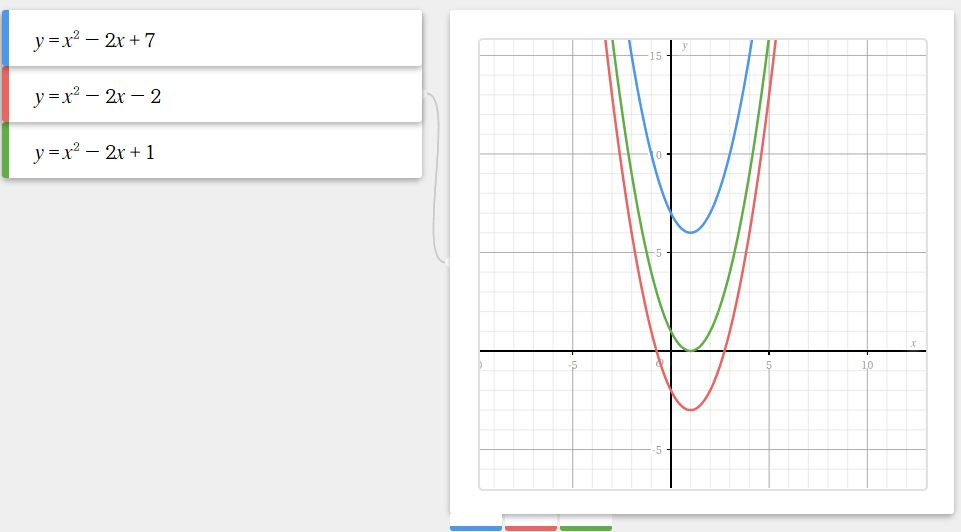
しばらくは頭の中が真っ白になった問題でした。( ^^;

では今日も１日の習慣を始めてます。小さな一歩・挑戦を試みています。