皆さん こんにちは、時空 解です。

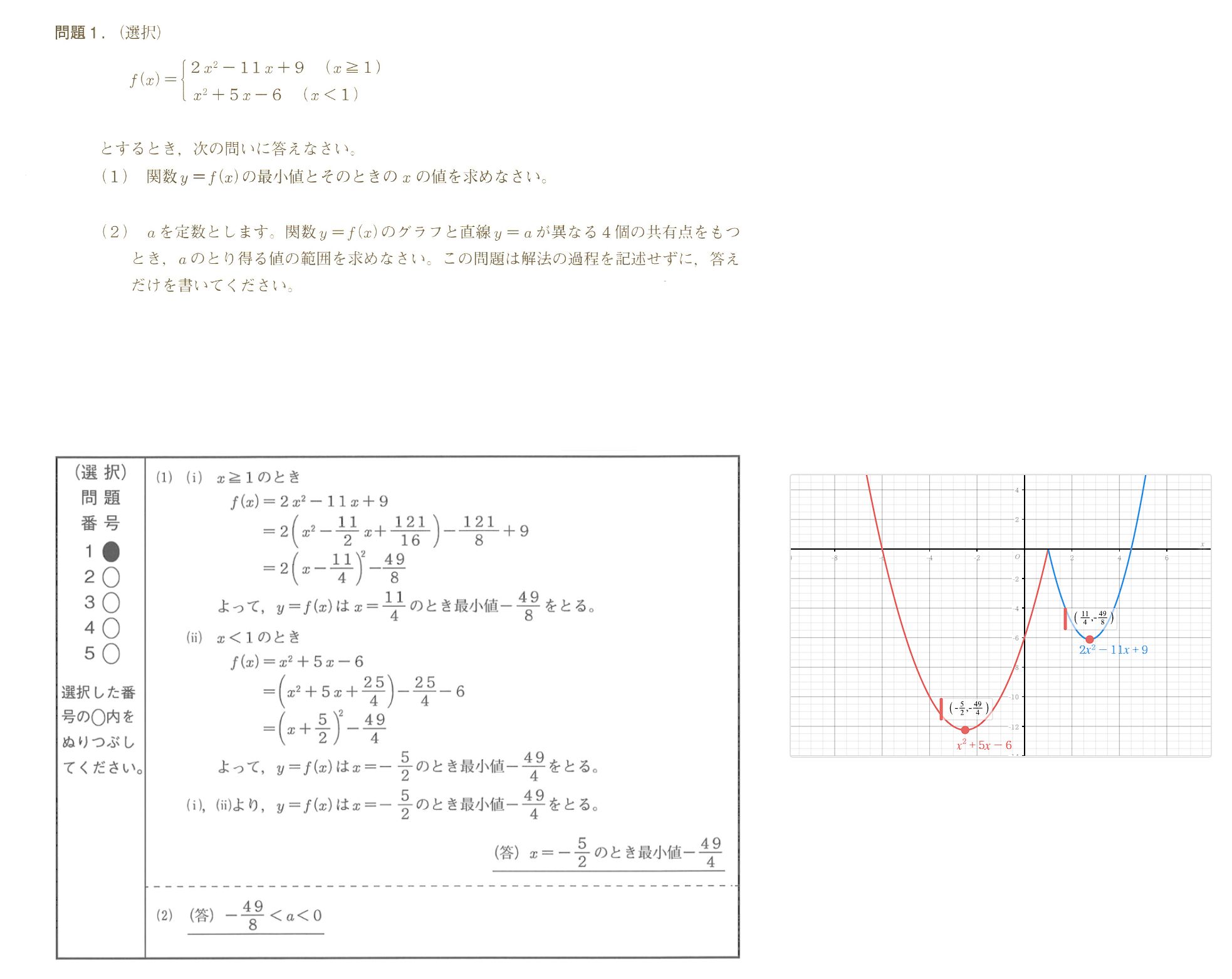
今日は表題のとおり、数学検定２級２次の問題１ (選択) について書いてみます。


この問題は与えられた式を完全平方することが出来れば、もう解けたも同然の問題でしたね。
詳細は右画像を参照ください。

でもね…設問 (2) を私はしくじりました。くそーっ！

そう言えば問題文に $ x $ の範囲と、それに対応する式が決められていました。
ですからね、画像に示したグラフからも分かるように、グラフが交差しているところから上 ( $ y > 0 $ ) は除外して考えなくてはなりません。

ですから設問 (2) の答は、右画像のとおり
　　　$ \displaystyle - \frac{ 49 }{ 8 } \lt a \lt 0 $
となりますが、私は
　　　$ \displaystyle - \frac{ 49 }{ 8 } \lt a \lt 0,~~0 \lt a $
と解答してしまったんです。

…それに今考えなおしてみると、$ y >0 $ の範囲でも二つのグラフが交わるところが有りそうなので、とにかく間違ってますね。＿|￣|○

うーむ… $ 0.4 $ 点くらい減点されて、ここは $ 0.6 $ 点と言うところかな？ ( ^^;

明日は問題２ (選択) を復習する予定です。