皆さん こんにちは、時空 解です。

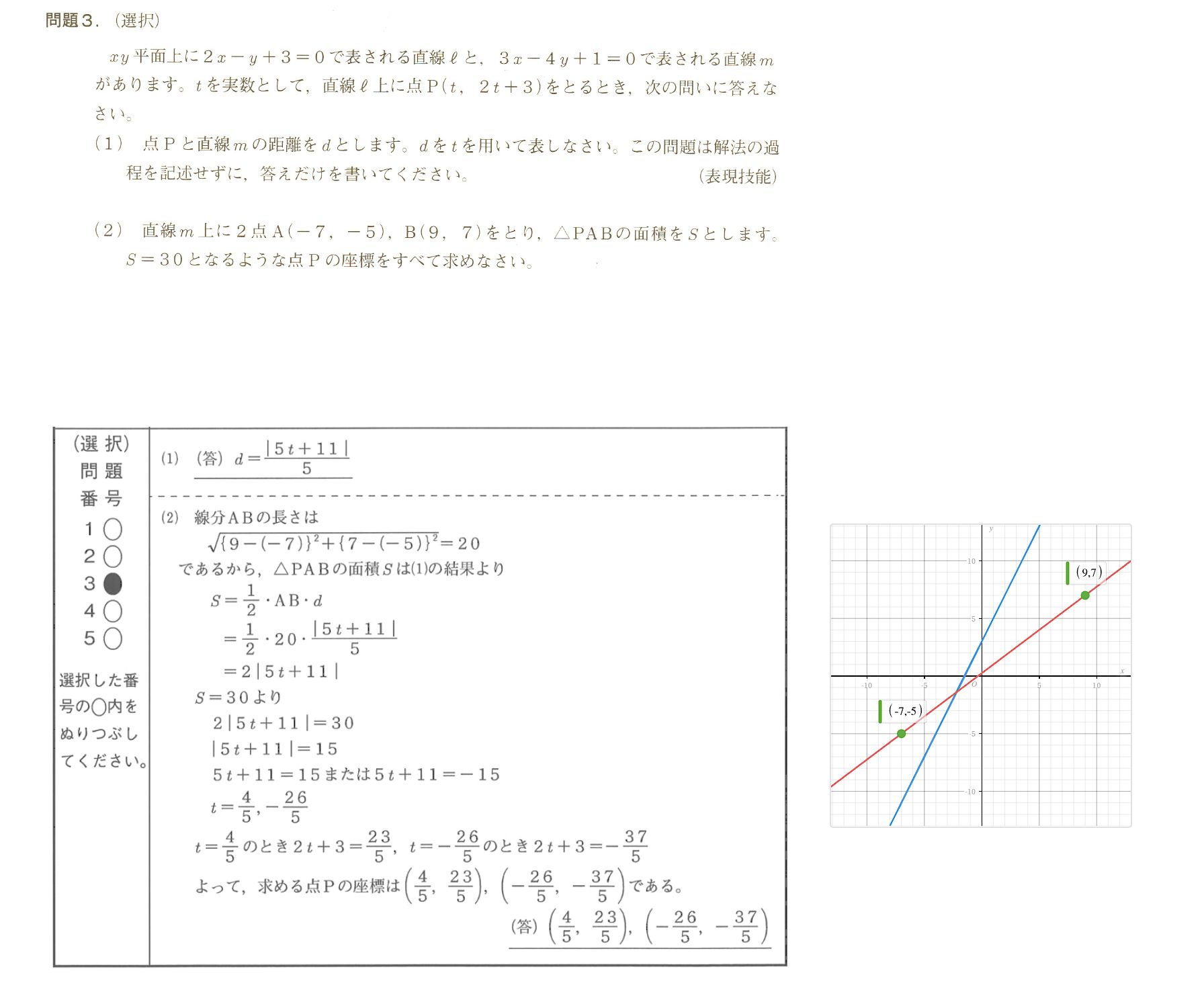
今日は表題のとおり、数学検定２級２次の問題３ (選択) について書いてみます。
問題とその模範解答は右図に示します。

この問題は「青チャート式数学II」の中の第３章。
・点と直線の距離の公式

上記が使いこなせるかを試す問題と言えます。

おっと！　　…そりゃまあおっしゃる通り。

方程式を立てて解けなくちゃいけませんし、３角関数の面積の公式も使いこなせないとね。
でも細かいことはともかく、重要なのは問題文を図示することでしょうか？

私はこれを怠りました…。＿|￣|○
点と直線の距離の公式を使って設問 (1) は解けたんですが…

設問 (2) を読んだ時に頭の中が "プチッ" とちょっと白くなりましてね。( ^^;
こう想っちゃったんです。
「あ、こりゃあ時間が掛かる問題だな…どうしよう」
とね。

でも改めてこの問題を見てみると、中学時代の自分なら当然のように図示していた問題だと想えました。
だけども "プチッ" と頭が白くなった理由は、与式の１次方程式が一般形で書かれている点でしょう。

直線 $ l $ 　　$ 2x -y +3 = 0 $
直線 $ m $　　$ 3x -4y +1 = 0 $

こんな形より

直線 $ l $ 　　$ y=2x+3 $
直線 $ m $　　$ y=\displaystyle \frac{ 3 }{ 4 } x + \frac{ 1 }{ 4 } $

と書かれていればね…すぐにグラフ化したのに…ま、言い訳ですけど ＿|￣|○

図示しようと想えば、直ぐにでも上記の変形はできますし、そしたら先に示した図中のグラフが描けたのにね。

これを描けば、
「おおっ、点 $ P $ までの距離が３角形の高さになるから、後は計算のみ」
と、楽しい気分で問題を解いていたことでしょう。

つまずくとしたら "点と直線の距離" を計算すると、距離 $ d $ が次のような形になるところのみ。
 
　　　$ d = \displaystyle \frac{ \left| 3t + (-4)(2t+3) + 1 \right| }{ \sqrt{ 3^2 + (-4)^2 } } = \frac{ \left| -5t -11 \right| }{ 5 } $

と、分子のところが $  \left| -5t -11 \right| $ なんてなってね。絶対記号とマイナス記号がとってもうっとうしい。
数学検定協会の模範解答ではマイナス記号が取られていますよね。

これは
　　　 $  \left| -5t -11 \right| = \left| -(5t +11) \right| =   \left| 5t +11 \right| $
と変形できますから問題が無いのです。

うーむ…設問 (1) の解答はやっぱり模範解答のように記述しないと減点されるんですかね？ ( ^^;
私は設問 (1) の解答として
　　　$ d = \displaystyle \frac{ \left| -5t -11 \right| }{ 5 } $

とかいちゃったし、設問 (2) は時間切れで記述できなかった…問題３の得点は $ 0.2 $ 点くらいかな？　

では今日も１日の習慣を始めてます。小さな一歩・挑戦を試みています。
(休日は充実した日々によって輝きますよね)