皆さん こんにちは、時空 解です。

今日は問題６を取り上げます。ここからは必須問題ですね。

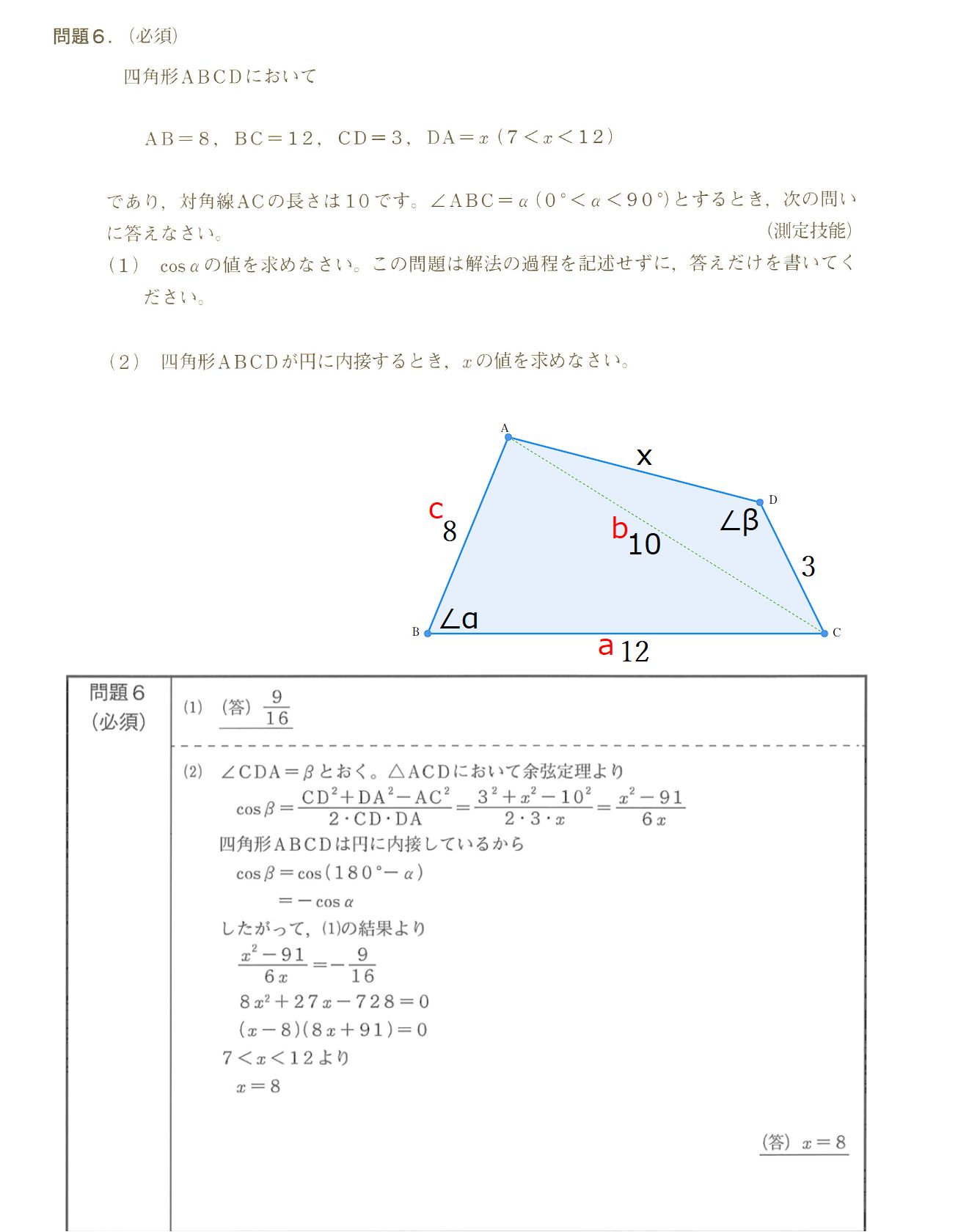
まずは問題とその答を右画像に示しておきます。
これは図形問題です。さっそく図示してみるのがいいです。

設問 (1) は、余弦定理を知っている方なら文字通り
「この問題は解法の過程を記述せずに、答えだけを書いてください。」
と指示が入るのが妥当だと分かりますよね。

$ \triangle ABC $ の３辺の長さと $ \angle α $ が分かっています。
したがって余弦定理より
　　　$ \cos α = \displaystyle \frac{b^2 -c^2 -a^2}{-2ca} = \frac{10^2 -8^2 -12^2}{-2 \cdot 8 \cdot 12} = \frac{9}{16} $

設問 (2) は、$ \angle β $ をどう求めるかです。
模範解答にあるように、余弦定理より $ \angle β $ と 各辺との関係式は書くことが出来ます。
でも、$ \angle β $ の数値が分からないと、辺 $ AD (x) $ を計算することが出来ませんよね。

そこで必要になるのが
数学Ａ、図形の性質より
・円に内接する４角形の性質

です。


これと、後は三角比の $ 180^\circ - \theta $ の性質ですよね。

この "円に内接する４角形の性質" と " $ 180^\circ - \theta $ " から
　　　$ \cos \beta = - \cos \alpha $
です。

私は検定中に $ \cos \beta = - \cos \alpha $ になかなか気付けませんでね…時間が掛かりました。＿|￣|○
でもこの問題６では $ 1 $ 点が貰えると思っていますが…うーむ

やっぱり $ 0.8 $ 点かな…記述に自信がないからね。( ^^;

では今日も１日の習慣を始めてます。小さな一歩・挑戦を試みています。
(休日は充実した日々によって輝きますよね)