皆さん こんにちは、時空 解です。

今日は問題７を取り上げます。第440回 数学検定２級２次 の最後の問題で、必須問題です。

まずは問題とその答を右画像に示しておきます。

この問題７もなかなか手強い問題でしたね、今日数学検定協会からご別成績票が送付されて来たのですが、全体の正解率が $ 38.8 \% $ と、７問中２番目に難しい問題と言う結果が出ています。
(ちなみに一番の不正解率だったのは問題３で $ 33.7 \% $ です)

模範解答を見てもなかなか意味を理解出来なかった私です。その理由は、$ x $ と $ a $ との関係をどう見たらいいのか、頭が混乱するからです。

でもね。これはグラフ化をしてみると
「あ、何だ…そう言う意図の問題か。気が付いていれば…」
と思うような問題だったと思います。

ポイントは
「 $ a $ の値を $ a= 4 $ と $ a = 6 $ と想定して、それぞれ２つの数式をグラフ化してみる」
と言う点です。

これをやってみたものを下に示します。


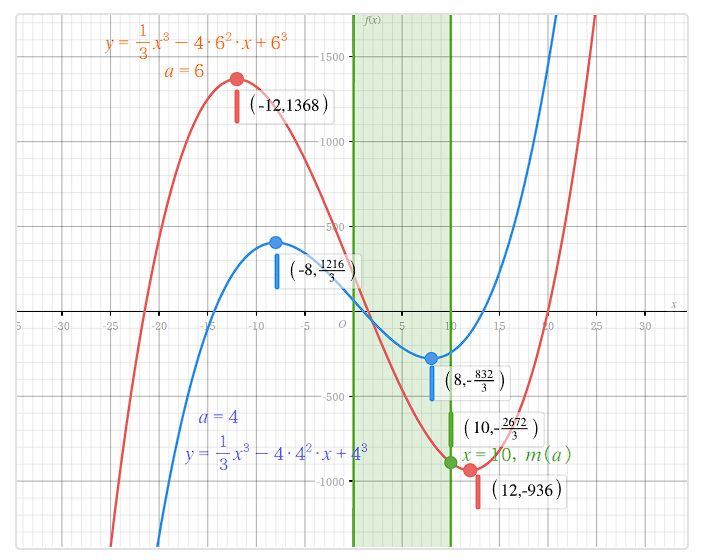
青いグラフが $ a = 4 $ の場合のグラフで、赤いグラフが $ a = 6 $ です。

グラフを描くには、３次方程式がどのような形をしているのかを知る必要があります。
そのために与式
　　　$ f(x) = \displaystyle \frac{1}{3} x^3 -4a^2 x + a^3 $ の微分
　　　$ f'(x) = x^2 -4a^2 = 0 $
を調べて極大値、極小値を求める必要があります。
この結果、極大値の時の $ x $ は $ x = -2a $。極小値の時は $ x = 2a $　　( $ a \gt 0 $ )
また $ x^3 $ の係数が $ \displaystyle \frac{1}{3} $ なのでグラフの形も決まります。

２つのグラフが頭の中で描けたならば、$ a = 0,~ 1,~ 2,~ 3 $ のグラフも見えてくるでしょう。
極大値と極小値との間が、$ a  $ が大きくなって行くに従って広がって行きます。

さて、グラフを目の前にして、改めて問題を読んでみると題意が見えてきます。

設問 (1) は $ 0 \leqq x \leqq 10 $ の範囲の最小値 m(a) を求める問題です。
グラフの緑の領域 ( $ 0 \leqq x \leqq 10 $ ) 内に極小値があることが見て取れるでしょう。
ですから、最小値は常に極小値 $ x = 2a $ のところと分かり、これを与式に代入するだけです。

設問 (2) の題意は
・ $ x = 10 $ の時の $ f(x) $ の値はどうなるのか？
と言う問いです。つまり $ a \gt 5 $ 、赤いグラフの場合のことを問うています。

最小値は極小値ではなく、$ f(10) $ の時の値となります。グラフではこの点を緑色の点で表してあります。
　　　 $ f(10) =m(a) = \displaystyle \frac{1}{3} 10^3 -4 \cdot a^2 \cdot 10 + a^3 $ 
　　　　　　　　$ = a^3 -40 a^2 + \displaystyle \frac{ 1000}{ 3} $

この問題は題意を見抜くためにグラフ化が必要なります。でも定数 $ a $ が障害となり、なかなかグラフ化できないところが難しい点でしょう。

では今日も１日の習慣を始めてます。小さな一歩・挑戦を試みています。
(休日は充実した日々によって輝きますよね)