時空 解 さんの日記
2017
2月
28
(火)
09:02
本文
みなさん、おはようございます。時空 解です。
4月16日(日) の数学検定3級に向けて、毎日ちょっとづつ数学の勉強をしています。
昨日の数学の予定は
・昨日の復習 ( p72 発展問題 )
・実用数学技能検定 要点整理3級 2-3 関数 y = ax二乗 (p74 ~p82)
でしたが、二番目に関しては学習できませんでした。と言うのも、p72 の発展問題をカルキングソフトを使って詳しく書いていた時間が掛かってしまったのです。
慣れないソフトを使うと、時間がかかりますね。
4月16日(日) の数学検定3級に向けて、毎日ちょっとづつ数学の勉強をしています。
昨日の数学の予定は
・昨日の復習 ( p72 発展問題 )
・実用数学技能検定 要点整理3級 2-3 関数 y = ax二乗 (p74 ~p82)
でしたが、二番目に関しては学習できませんでした。と言うのも、p72 の発展問題をカルキングソフトを使って詳しく書いていた時間が掛かってしまったのです。
慣れないソフトを使うと、時間がかかりますね。
ま、今日は p71 発展問題、書籍の答えと私のなりの答えをここに書いておきます。時間のある方は私の答えにも目を通してみてくださいね。ごちゃごちゃとした説明ですが。書籍のようにシンプルな解説がいいのか、それとも自分の解説のように長いけれど丁寧(のつもり)な解説の方が良いのか?
ともかく自分なりに解説をする練習を繰り返して行くつもりでいます。
いつか "シンプル" かつ "文系の人にも理解できる" 解説が書けるようになると良いなぁと思っています。
ともかく自分なりに解説をする練習を繰り返して行くつもりでいます。
いつか "シンプル" かつ "文系の人にも理解できる" 解説が書けるようになると良いなぁと思っています。
では、p72 発展問題、問題と書籍の答え、それと私なりの答えを下記に示します。
----------------------
発展問題 (p72)
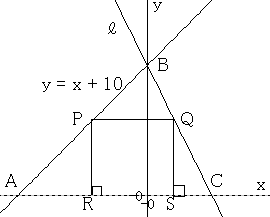 右の図のように直線 y = x + 10 と x軸、y軸との交点をそれぞれ A, B とし、点 B と 点 C (5, 0) を通る直線を ℓ とします。線分 AB 上に点 P, 線分 BC 上に点 Q をとり、2点 P, Q から x 軸に引いた垂線と x軸との交点をそれぞれ R, S として、次の問いに答えなさい。
右の図のように直線 y = x + 10 と x軸、y軸との交点をそれぞれ A, B とし、点 B と 点 C (5, 0) を通る直線を ℓ とします。線分 AB 上に点 P, 線分 BC 上に点 Q をとり、2点 P, Q から x 軸に引いた垂線と x軸との交点をそれぞれ R, S として、次の問いに答えなさい。
(1) 直線 ℓ の式を求めなさい。
(2) 四角形 PRSQ が正方形になるとき、1編の長さを求めなさい。ただし、座標の1めもりを1cm とします。
----------
書籍の答え
(1) 切片が 10 なので、求めり直線 ℓ の式は
y = ax + 10 … (1)
点 C を通るので、(1) に x = 5, y = 0 を代入して、
0 = 5a + 10 a = -2
したがって y = -2x + 10
答え y = -2x + 10
発展問題 (p72)
 右の図のように直線 y = x + 10 と x軸、y軸との交点をそれぞれ A, B とし、点 B と 点 C (5, 0) を通る直線を ℓ とします。線分 AB 上に点 P, 線分 BC 上に点 Q をとり、2点 P, Q から x 軸に引いた垂線と x軸との交点をそれぞれ R, S として、次の問いに答えなさい。
右の図のように直線 y = x + 10 と x軸、y軸との交点をそれぞれ A, B とし、点 B と 点 C (5, 0) を通る直線を ℓ とします。線分 AB 上に点 P, 線分 BC 上に点 Q をとり、2点 P, Q から x 軸に引いた垂線と x軸との交点をそれぞれ R, S として、次の問いに答えなさい。(1) 直線 ℓ の式を求めなさい。
(2) 四角形 PRSQ が正方形になるとき、1編の長さを求めなさい。ただし、座標の1めもりを1cm とします。
----------
書籍の答え
(1) 切片が 10 なので、求めり直線 ℓ の式は
y = ax + 10 … (1)
点 C を通るので、(1) に x = 5, y = 0 を代入して、
0 = 5a + 10 a = -2
したがって y = -2x + 10
答え y = -2x + 10
(2) 点 P, Q の x 座標をそれぞれ p, q とすると、P(p, p+10), Q(q, -2q+10), R(p, 0), S(q, 0) と表せる。
PR = p+10, RS = q-p, QS = -2q+10 であるから、
PR = QS より、p + 10 = -2q + 10 p = -2q …(1)
PR = RS より、p + 10 = q - p q = 2p + 10 …(2)
(1)を(2)に代入して、q = 2 × -2q + 10
5q = 10 q = 2
q = 2 を(1)に代入して、p = -2 + 2 = -4
求める1辺の長さは、RS = 2 - -4 = 6(cm)
答え 6cm
---------------------------
---------------------------
私の答え
(1) の答えは割愛します。書籍の答えと同じです。
(2) 四角形 PRSQ が正方形になると言う事は正方形の性質上、全ての辺の長さが等しい。これより
PR = RS, PR = QS
これを踏まえ PR, RS, QS の線分の長さを座標点の値から求める。
まずは点 P, R, S, Q それぞれの座標点がどのようになるのかを見てみると、点 R と S は x軸上にあるので、y軸の値が 0 と分かる。
したがって
P = (?, ?)
R = (?, 0)
S = (?, 0)
Q = (?, ?)
と書ける。
また、線分 PR は y軸に平行なので、x軸の値は同じはずである。この x軸の値を p と仮定すると 点 P, R は
P = (p, ?)
R = (p, 0)
線分 QS も y軸に平行なので、x軸の値が同じばすであるので、どうように x軸の値を q と仮定すると 点 S, Q は
S = (q, 0)
Q = (q, ?)
ここで点 P は y = x + 10上にあり、点 Q は y = -2x + 10 上にある。これより点 P, Q それぞれの y座標の値を p, q を使って表せる。
PR = p+10, RS = q-p, QS = -2q+10 であるから、
PR = QS より、p + 10 = -2q + 10 p = -2q …(1)
PR = RS より、p + 10 = q - p q = 2p + 10 …(2)
(1)を(2)に代入して、q = 2 × -2q + 10
5q = 10 q = 2
q = 2 を(1)に代入して、p = -2 + 2 = -4
求める1辺の長さは、RS = 2 - -4 = 6(cm)
答え 6cm
---------------------------
---------------------------
私の答え
(1) の答えは割愛します。書籍の答えと同じです。
(2) 四角形 PRSQ が正方形になると言う事は正方形の性質上、全ての辺の長さが等しい。これより
PR = RS, PR = QS
これを踏まえ PR, RS, QS の線分の長さを座標点の値から求める。
まずは点 P, R, S, Q それぞれの座標点がどのようになるのかを見てみると、点 R と S は x軸上にあるので、y軸の値が 0 と分かる。
したがって
P = (?, ?)
R = (?, 0)
S = (?, 0)
Q = (?, ?)
と書ける。
また、線分 PR は y軸に平行なので、x軸の値は同じはずである。この x軸の値を p と仮定すると 点 P, R は
P = (p, ?)
R = (p, 0)
線分 QS も y軸に平行なので、x軸の値が同じばすであるので、どうように x軸の値を q と仮定すると 点 S, Q は
S = (q, 0)
Q = (q, ?)
ここで点 P は y = x + 10上にあり、点 Q は y = -2x + 10 上にある。これより点 P, Q それぞれの y座標の値を p, q を使って表せる。
まずは P = (p, ? ) について、点 P は y = x + 10 上にあるので ? = p + 10
したがって
P = (p, p + 10)
つぎに Q = (q, ? ) について、点 Q は y = -2x + 10 上にあるので ? = -2q + 10
したがって
Q = (q, -2q + 10)
となる。
したがって
P = (p, p + 10)
つぎに Q = (q, ? ) について、点 Q は y = -2x + 10 上にあるので ? = -2q + 10
したがって
Q = (q, -2q + 10)
となる。
これで正方形 PRSQ のすべての点の座標が p, q で表現で来た。
P = (p, p + 10)
R = (p, 0)
S = (q, 0)
Q = (q, -2q + 10)
上記の座標値より四角形のそれぞれの辺の長さを求める事が出来る。
PR, RS, QS を求めると
RP = (点 P の y値 - 点 R の y値) = p + 10 - 0 = p + 10
RS = (点 S の x値 - 点 R の x値) = q - p = q - p
QS = (点 Q の y値 - 点 S の y値) = -2q + 10 - 0 = -2q + 10
正方形の性質より PR = RS, PR = QS なので、次の連立方程式が、成り立つはずである。
PR = RS より p + 10 = q - p …(1)
PR = QS より p + 10 = -2q + 10 …(2)
上式 (1), (2) より p, q を求めると
p = -4, q = 2
となる。
P = (p, p + 10)
R = (p, 0)
S = (q, 0)
Q = (q, -2q + 10)
上記の座標値より四角形のそれぞれの辺の長さを求める事が出来る。
PR, RS, QS を求めると
RP = (点 P の y値 - 点 R の y値) = p + 10 - 0 = p + 10
RS = (点 S の x値 - 点 R の x値) = q - p = q - p
QS = (点 Q の y値 - 点 S の y値) = -2q + 10 - 0 = -2q + 10
正方形の性質より PR = RS, PR = QS なので、次の連立方程式が、成り立つはずである。
PR = RS より p + 10 = q - p …(1)
PR = QS より p + 10 = -2q + 10 …(2)
上式 (1), (2) より p, q を求めると
p = -4, q = 2
となる。
正方形の1辺の長さを RS = q - p より求めると 6cm となる。
RP, QS から求めても同様に 6cm となる。
答え 6cm
---------------------------
RP, QS から求めても同様に 6cm となる。
答え 6cm
---------------------------
ここまで目を通して頂き、ありがとうございます。
こうしてブログに載せてみると、やはり私の解説は長すぎる感がありますね。
こうしてブログに載せてみると、やはり私の解説は長すぎる感がありますね。
上手に解説できるようになるかなぁ…。
では今日の数学の予定は
・実用数学技能検定 要点整理3級 2-3 関数 y = ax二乗 (p74 ~p82)
です。
応援してね。
千里の道も一歩から…。
(ポチッと右のバナーをクリックしてね)
「良い習慣化計画」
朝は七時に起きます。
夜は11時に寝ます。
数学、物理の勉強をします。
ブログを毎日更新します。
勉強会の動画は YouTube チャンネル でご覧になれます。( 更新なし
・実用数学技能検定 要点整理3級 2-3 関数 y = ax二乗 (p74 ~p82)
です。
応援してね。
千里の道も一歩から…。
(ポチッと右のバナーをクリックしてね)
「良い習慣化計画」
朝は七時に起きます。
夜は11時に寝ます。
数学、物理の勉強をします。
ブログを毎日更新します。
勉強会の動画は YouTube チャンネル でご覧になれます。( 更新なし
閲覧(5334)
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |





 前の日記
前の日記



