皆さん こんにちは、時空 解です。

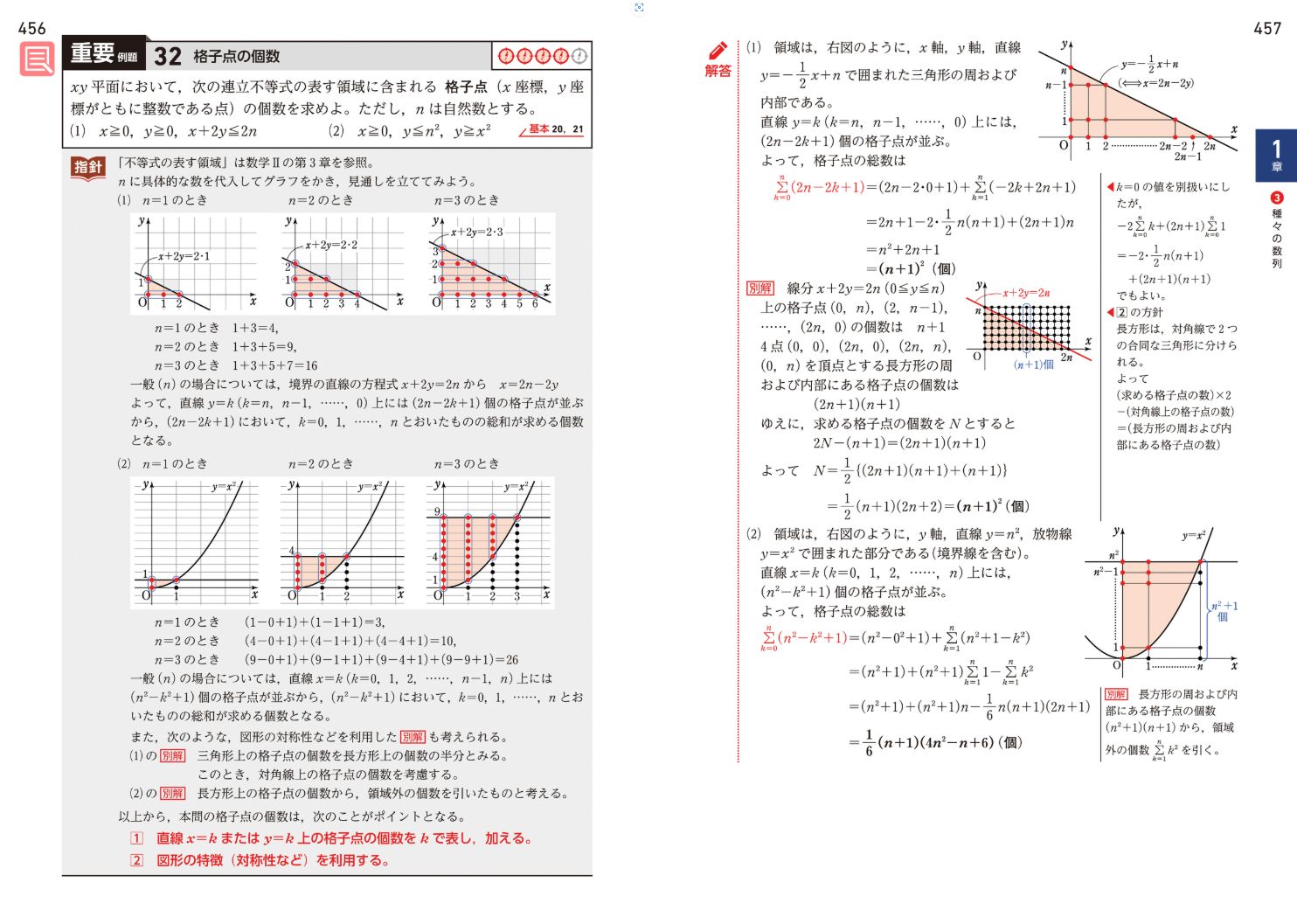
表題に示した数列に関する問題、【重要例題３２：格子点の個数】
この問題の設問 (1) を解くための数式 $ 2n -2k +1 $ がなかなか立てられません。

うーむ…難しい。＿|￣|○

この $ 2n -2k +1 $ を立てるための "感覚" が自分の頭の中には無いように感じししまいほどです。

でもその理由は一つ。

この数式を立てるための数学的な "直感" が育まれていないのでしょうね。( ^^;

やっぱり直感を育むためにはたくさんの問題を解くしかありません。

と言うことで…
$ 2n -2k +1 $ と言う式は設問 (1) の $ x +2y \leqq 2n $ の式に対するものですすが…

合わせて設問 (2) に付いて見てみると…
$ y = x^2 $ に対して $ n^2 -k^2 +1 $ と言う式ですね。

ついでに、この重要例題３２に続く、練習問題３２についても見てみると
 

練習問題３２の設問 (1) に付いては $ x +3y \leqq 3n $ から察するに $ x : y = 3 : 1 $ なのでね…。
うーむ。

それと $ x +3y \leqq 3n $ の直線の傾きはどうなるかと言うと…。　…？
やっぱりグラフ化して、まずは数個検証して見ないとイメージ湧きませんね。( ^^;


と言うことで下図に書いたグラフを示します。




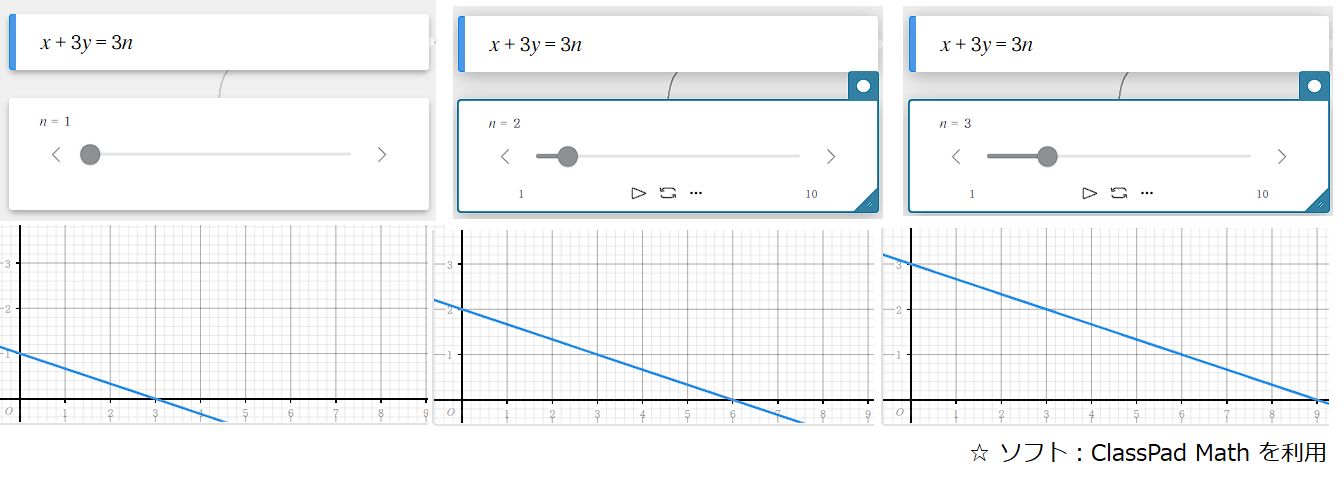
おおっ！　やっぱりグラフを描くと見えてきますね。

これなら横方向に格子点が数列的にならびますから、つまりは $ y = k $ で $ x $ 軸上に並ぶ点をシグマ計算すればいいようです。
となると…これからシグマする数式は…。

　　　うーむ、ここが難しい。＿|￣|○

$ 3 $ 倍するのは $ k $ なのか $ n $ なのか？

　…$ \bigcirc \cdot \bigtriangleup -  3 \cdot \square + 1 $

　　おおっ！　

こうやって考えてくると分かって来ます、両方とも $ 3 $ 倍すると式が成立します。

と言うことでシグマする数式は
　　　$ 3n - 3k +1 $
で良さそうです。

この式をグラフに当てはめてみると、正しそうなことが分かります。

つまり格子点の数は

　　　$ \displaystyle \sum_{ k = 0 }^{ n } (3n - 3k +1) $

ここから、シグマ記号は $ k=1 $ からなので $ k=0 $ について

　　　$ 3 \cdot n - 3 \cdot 0 +1 = 3n +1 $

それと
　　　$ \displaystyle \sum_{ k = 1 }^{ n }(3n - 3k +1) = \displaystyle \sum_{ k = 1 }^{ n }(3n +1) -3 \sum_{ k = 1 }^{ n }k $
　　　　　　　　　　　　$ = n(3n +1) -3 \cdot \displaystyle \frac{ 1 }{ 2 }n(n+1) $

上記の両方を足し合わせて

　　　$ 3n +1 + n(3n +1) -3 \cdot \displaystyle \frac{ 1 }{ 2 }n(n+1) = 3n +1 +3n^2 +n - \displaystyle \frac{ 3 }{ 2 }n^2 - \frac{3}{2}n $
　　　　　　　　　　　　　　　　　　　　　　$ = \displaystyle \frac{ 1 }{2 } \left( 6n +2 +6n^2 + 2n -3n^2 -3n \right) $
　　　　　　　　　　　　　　　　　　　　　　$ = \displaystyle \frac{1}{2} \left( 3n^2 +5n +2 \right)  $
　　　　　　　　　　　　　　　　　　　　　　$ = \displaystyle \frac{1}{2} (3n +2)(n +1) $

となります。
やれやれ、答は合ってました。

設問 (2) は明日にします。もうこんな時間だ…