時空 解 さんの日記
2025
6月
3
(火)
10:50
本文
皆さん こんにちは、時空 解です。
今日は一昨日の続きです。
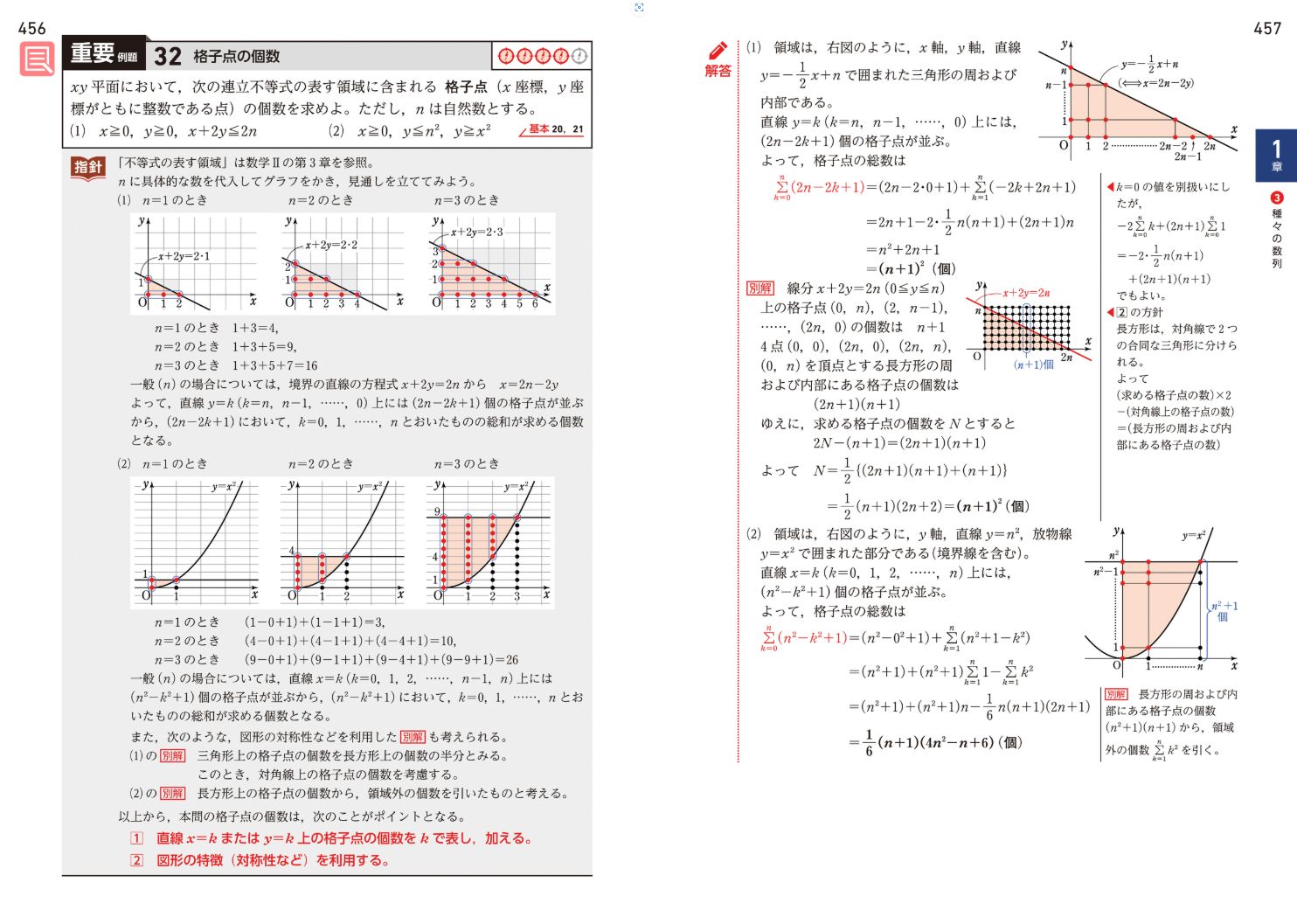
まず重要例題32 (右画像参照) と練習問題32 (下記) を提示しておきましょう。
さて、今日は上記2つの問題から、それぞれ設問 (2) を取り上げてみます。
取り上げるに当たって、始めに両方の問題をグラフ化しておきましょう。
重要例題32 設問 (2) のグラフ

練習問題32 設問 (2) のグラフ
格子点問題を解くカギは、やっぱり
・グラフ化をしてみて、格子点の数を数えてみる
と言うのが第一歩になるでしょう。
格子の点の数は $ x $ 軸、$ y $ 軸のどちらに沿って数えると整数的 (領域の両端に格子点が有る) に変化しているでしょうか?
グラフ化してみるとそれが見えてきますよね。
今回、両方とも $ x= 1,~2,~3,~4,~ \dotsm $ として見て行くと格子点の数がちゃんと領域に収まっています。
重要例題32 設問 (2) の場合、$ n = 4 $ のグラフについて格子点の数を見てみると
格子の数
$ x = 0 $ → $ 16 - ~0 + 1 $
$ x = 1 $ → $ 16 - ~1 + 1 $
$ x = 2 $ → $ 16 - ~4 + 1 $
$ x = 3 $ → $ 16 - ~9 + 1 $
$ x = 4 $ → $ 16 - 16 + 1 $
と書くことが出来ます。
上記のように格子の数を書き出すためには、
・$ 16 $ が $ n $ に対応して、引く数は変数 $ y = k $ と見なす
と言うことです。
まぁここが慣れないと難しいのですけどね。( ^^;
慣れるためにはたくさんの問題を解くしかありません。
練習問題32についても見てみましょう。
こちらはちょっと複雑になります。なんと言っても双曲線が2本になりますから、グラフをよく見る必要がありますよね。
( $ y $ 軸の目盛りが $ 2 $ 飛びになっていることに注意 )
重要例題同様、練習問題32 設問 (2) についても、$ n = 4 $ のグラフについて格子点の数を見てみると
格子の数
$ x = 0 $ → $ 0 - ~0 + 1 $
$ x = 1 $ → $ 2 - ~1 + 1 $
$ x = 2 $ → $ 8 - ~4 + 1 $
$ x = 3 $ → $ 18 - ~9 + 1 $
$ x = 4 $ → $ 32 - 16 + 1 $
と書くことが出来ます。
でも、もう少し数式を書くために分かり易くすると
格子の数
$ x = 0 $ → $ 0 - ~0 + 1 $
$ x = 1 $ → $ 2 \cdot 1 - ~1 + 1 $
$ x = 2 $ → $ 2 \cdot 4 - ~4 + 1 $
$ x = 3 $ → $ 2 \cdot 9 - ~9 + 1 $
$ x = 4 $ → $ 2 \cdot 16 - 16 + 1 $
と出来ますよね。
これで両方のシグマ計算用の式を書く準備が出来ました。

・重要例題32 設問 (2)
$ n^2 -k^2 +1 $
・練習問題32 設問 (2)
$ 2k^2 -k^2 +1 $
$ = k^2 +1 $
これで両方の問題の計算式を立てることができます。
・重要例題32 設問 (2)
$ k =0 $ $ k =1,~2,~3,~4, \dotsm $
$ \displaystyle \sum_{ k = 0 }^{ n }(n^2 -k^2 +1) = (n^2 +1) + \sum_{ k = 1 }^{ n }(n^2 -k^2 +1) $
$ = (n^2 +1) + \displaystyle \sum_{ k = 1 }^{ n }(n^2 -k^2 +1) $
$ = (n^2 +1) + \displaystyle \sum_{ k = 1 }^{ n }(n^2 +1) - \sum_{ k = 1 }^{ n }k^2 $
$ = (n^2 +1) + n(n^2 +1) - \displaystyle \frac{ 1 }{ 6 } n(n +1)(2n +1) $
整理すると
$ \displaystyle \frac{ 1 }{ 6 }(n +1)(4n^2 -n +6) $
・練習問題32 設問 (2)
$ k =0 $ $ k =1,~2,~3,~4 , \dotsm $
$ \displaystyle \sum_{ k = 0 }^{ n }(k^2 +1) = 1 + \sum_{ k = 1 }^{ n }(k^2 +1) $
$ = 1 + \displaystyle \frac{ 1 }{ 6 } n(n +1)(2n +1) $
整理すると
$ \displaystyle \frac{ 1 }{ 6 }(n +1)(2n^2 +n +1) $
練習問題23の答も右画像に示しておきます。
では今日も1日の習慣を始めてます。小さな一歩・挑戦を試みています。
(休日は充実した日々によって輝きますよね)

今日は一昨日の続きです。
まず重要例題32 (右画像参照) と練習問題32 (下記) を提示しておきましょう。
練習問題32
$ xy $ 平面において、次の連立不等式の表す領域に含まれる格子点の個数を求めよ。
ただし、$ n $ は自然数とする。
(1) $ x \geqq 0,~~y \geqq 0,~~x +3y \leqq 3n $ (2) $ 0 \leqq x \leqq n,~~y \geqq x^2,~~y \leqq 2x^2 $
$ xy $ 平面において、次の連立不等式の表す領域に含まれる格子点の個数を求めよ。
ただし、$ n $ は自然数とする。
(1) $ x \geqq 0,~~y \geqq 0,~~x +3y \leqq 3n $ (2) $ 0 \leqq x \leqq n,~~y \geqq x^2,~~y \leqq 2x^2 $
さて、今日は上記2つの問題から、それぞれ設問 (2) を取り上げてみます。
取り上げるに当たって、始めに両方の問題をグラフ化しておきましょう。
重要例題32 設問 (2) のグラフ

練習問題32 設問 (2) のグラフ

格子点問題を解くカギは、やっぱり
・グラフ化をしてみて、格子点の数を数えてみる
と言うのが第一歩になるでしょう。
格子の点の数は $ x $ 軸、$ y $ 軸のどちらに沿って数えると整数的 (領域の両端に格子点が有る) に変化しているでしょうか?
グラフ化してみるとそれが見えてきますよね。
今回、両方とも $ x= 1,~2,~3,~4,~ \dotsm $ として見て行くと格子点の数がちゃんと領域に収まっています。
重要例題32 設問 (2) の場合、$ n = 4 $ のグラフについて格子点の数を見てみると
格子の数
$ x = 0 $ → $ 16 - ~0 + 1 $
$ x = 1 $ → $ 16 - ~1 + 1 $
$ x = 2 $ → $ 16 - ~4 + 1 $
$ x = 3 $ → $ 16 - ~9 + 1 $
$ x = 4 $ → $ 16 - 16 + 1 $
と書くことが出来ます。
上記のように格子の数を書き出すためには、
・$ 16 $ が $ n $ に対応して、引く数は変数 $ y = k $ と見なす
と言うことです。
まぁここが慣れないと難しいのですけどね。( ^^;
慣れるためにはたくさんの問題を解くしかありません。
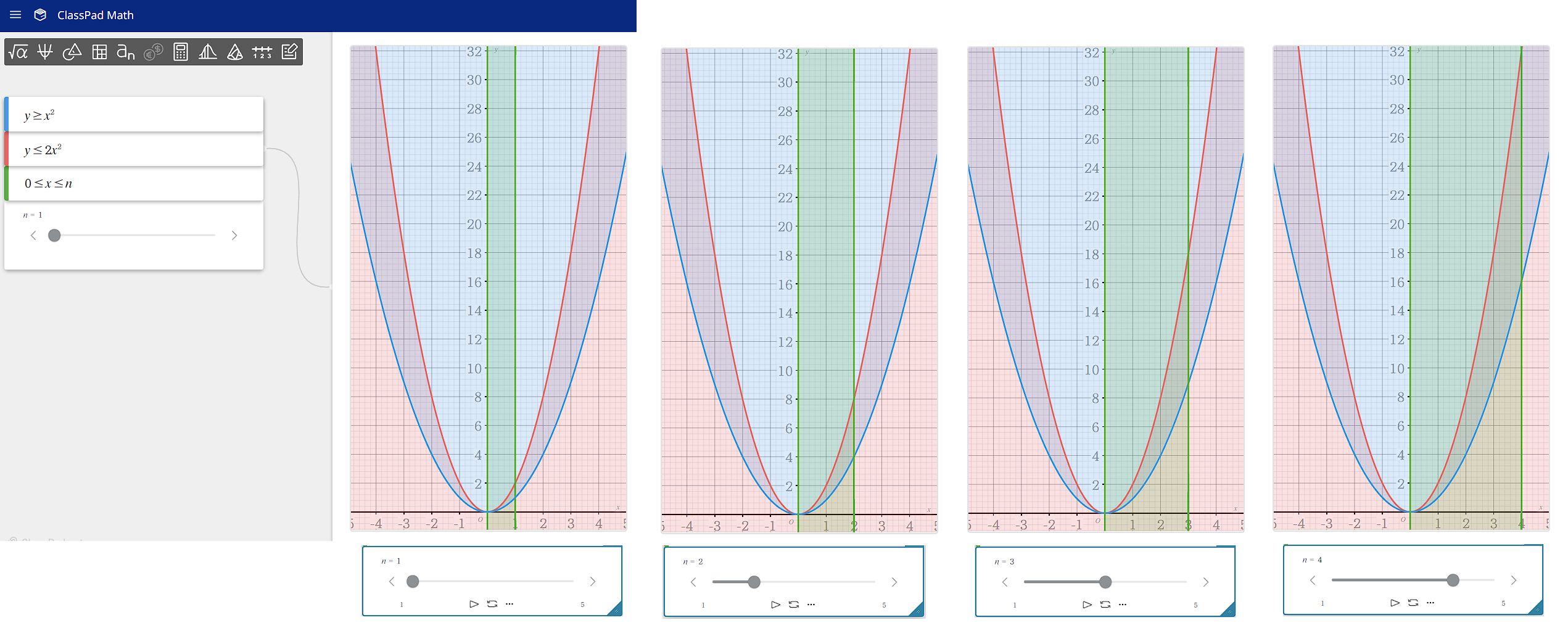
練習問題32についても見てみましょう。
こちらはちょっと複雑になります。なんと言っても双曲線が2本になりますから、グラフをよく見る必要がありますよね。
( $ y $ 軸の目盛りが $ 2 $ 飛びになっていることに注意 )
重要例題同様、練習問題32 設問 (2) についても、$ n = 4 $ のグラフについて格子点の数を見てみると
格子の数
$ x = 0 $ → $ 0 - ~0 + 1 $
$ x = 1 $ → $ 2 - ~1 + 1 $
$ x = 2 $ → $ 8 - ~4 + 1 $
$ x = 3 $ → $ 18 - ~9 + 1 $
$ x = 4 $ → $ 32 - 16 + 1 $
と書くことが出来ます。
でも、もう少し数式を書くために分かり易くすると
格子の数
$ x = 0 $ → $ 0 - ~0 + 1 $
$ x = 1 $ → $ 2 \cdot 1 - ~1 + 1 $
$ x = 2 $ → $ 2 \cdot 4 - ~4 + 1 $
$ x = 3 $ → $ 2 \cdot 9 - ~9 + 1 $
$ x = 4 $ → $ 2 \cdot 16 - 16 + 1 $
と出来ますよね。
これで両方のシグマ計算用の式を書く準備が出来ました。

・重要例題32 設問 (2)
$ n^2 -k^2 +1 $
・練習問題32 設問 (2)
$ 2k^2 -k^2 +1 $
$ = k^2 +1 $
これで両方の問題の計算式を立てることができます。
・重要例題32 設問 (2)
$ k =0 $ $ k =1,~2,~3,~4, \dotsm $
$ \displaystyle \sum_{ k = 0 }^{ n }(n^2 -k^2 +1) = (n^2 +1) + \sum_{ k = 1 }^{ n }(n^2 -k^2 +1) $
$ = (n^2 +1) + \displaystyle \sum_{ k = 1 }^{ n }(n^2 -k^2 +1) $
$ = (n^2 +1) + \displaystyle \sum_{ k = 1 }^{ n }(n^2 +1) - \sum_{ k = 1 }^{ n }k^2 $
$ = (n^2 +1) + n(n^2 +1) - \displaystyle \frac{ 1 }{ 6 } n(n +1)(2n +1) $
整理すると
$ \displaystyle \frac{ 1 }{ 6 }(n +1)(4n^2 -n +6) $
・練習問題32 設問 (2)
$ k =0 $ $ k =1,~2,~3,~4 , \dotsm $
$ \displaystyle \sum_{ k = 0 }^{ n }(k^2 +1) = 1 + \sum_{ k = 1 }^{ n }(k^2 +1) $
$ = 1 + \displaystyle \frac{ 1 }{ 6 } n(n +1)(2n +1) $
整理すると
$ \displaystyle \frac{ 1 }{ 6 }(n +1)(2n^2 +n +1) $
練習問題23の答も右画像に示しておきます。
では今日も1日の習慣を始めてます。小さな一歩・挑戦を試みています。
(休日は充実した日々によって輝きますよね)
閲覧(2863)
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |





 前の日記
前の日記



