時空 解 さんの日記
2025
6月
28
(土)
22:14
本文
皆さん こんにちは、時空 解です。
今日は理解するのを後回してしていたことを思い出しました。不等式についてです。
それは
・不等式どうしを引き算してはいけないのは何故か?
です。

朝に復習として「青チャート式数学I 第1章:数と式、第4節:1次不等式」の基本例題33をやっていたんですよね。
自分でも驚きましたが、どう考えていいやら全く分からず…始めは頭が真っ白でした。
しばらくして、設問の (1) は何とか分かってきましたが、設問 (2) に付いてはね…本当にお手上げ。( ^^;
一応自分なりに答は出してみたものの、予想通り間違った答でした。_| ̄|○
この設問 (2) に対して正しい解答をするためにも、先に上げた
・不等式どうしを引き算してはいけないのは何故か?
その理由をちゃんと理解しなければなりませんでした。
青チャート式数学の解説動画にも、この理由には触れておらずただ単に
「引き算をする、各辺を引くと言うのは上手く行かないんです。(中略) 基本の考えとして各辺で足し算する」
と、コメントを付けているのみです。
ここを深堀すると、ちょっと解説が長くなってしまうからでしょうね。
と言うことで、自分なりに納得するためには、シンプル問題に置き換えてかんがえてみることでしょう。
こんな問題について考えてみました。
この問題…昨日までの私の頭では、下記のような答になってしまいます。
「$ x -y $ なんだから、まず最小値は $ 1 -4 $ で $ -3 $ 。最大値は $ 2 -7 $ で $ -5 $」
つまり答は $ -3 \lt x -y \lt -7 $
これは不等号の向きからしておかしいですよね。_| ̄|○
じゃあ不等式の向きを変えれば OK かと申しますと…これも違います。
どうしてこうなっちゃうのかを考えるためには、私は下記のように数直線を描いてみた次第です。
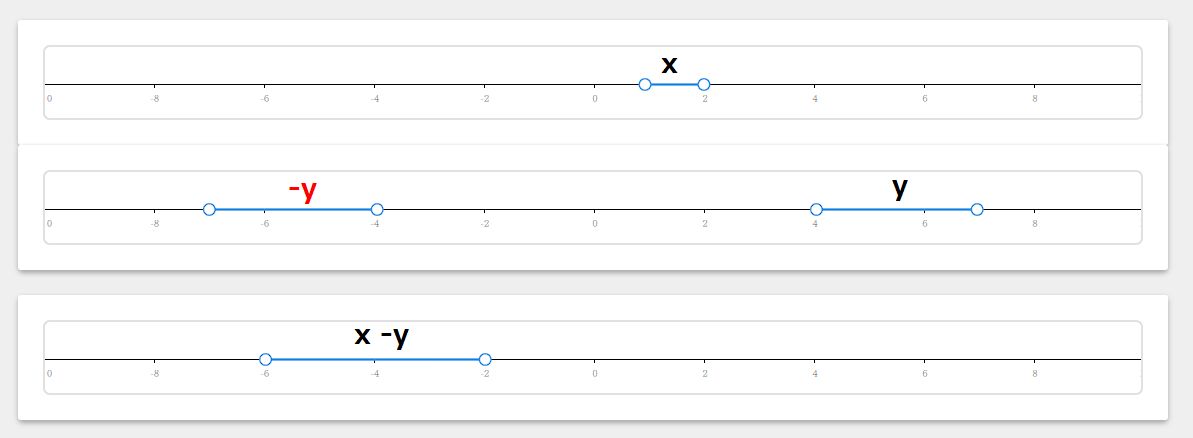
これを眺めながらやっと腑に落ちるようになりました。
$ x -y $ について、この値の最小値が左側、そして最大値が右側にくればいいんですよね。
言いたいことは、下記の式で伝わりますかな?
最小値 $ \lt x -y \lt $ 最大値
この最小値と最大値を求めるためには、どうしたらいいでしょうか?
そう考えると見えてきますよね。
まず最小値は、$ x $ が取りうる範囲の最小値から $ y $ が取りうる範囲の最大値を引けば出てきますよね。
$ 1 -7 = -6 $
つぎに最大値は、$ x $ が取りうる範囲の最大値から $ y $ が取りうる範囲の最小値を引けば出てきます。
$ 2 -4 = -2 $
つまり答は $ -6 \lt x -y \lt -2 $
さて、こうしてみると
・最小値を計算するのに、$ x,~y $ の最小値と最大値。
・最大値を計算するのに、、$ x,~y $ の最大値と最小値。
と言った具合にややこしい思考が必要になります。
それを解消するには、青チャート式数学の解説動画でコメントしているように、
「各辺で足し算できるような形にして計算する」
なんですよね。
$ y $ の方の範囲を各辺で足し算できるようにするためには、$ -1 $ を範囲指定の式に掛けてやればいいですよね。
$ -7 \lt -y \lt -4 $
こうしてやれば、$ x -y $ の範囲は、
$ ~1 \lt ~~x \lt ~2 $
$~+ -7 \lt -y \lt -4 $
-----------------------
$ -6 \lt x -y \lt -2 $
では今日も1日の習慣を始めてます。小さな一歩・挑戦を試みています。
(休日は充実した日々によって輝きますよね)
今日は理解するのを後回してしていたことを思い出しました。不等式についてです。
それは
・不等式どうしを引き算してはいけないのは何故か?
です。

朝に復習として「青チャート式数学I 第1章:数と式、第4節:1次不等式」の基本例題33をやっていたんですよね。
・基本例題33
$ x,~y $ を正の整数とする。$ x,~3x +2y $ を小数第1位で四捨五入すると、それぞれ $ 6,~21 $ になるという。
(1) $ x $ の値の範囲を求めよ。 (2) $ y $ の値の範囲を求めよ。
解答は右画像。解説動画はこちら → 設問 (1)、設問 (2)
$ x,~y $ を正の整数とする。$ x,~3x +2y $ を小数第1位で四捨五入すると、それぞれ $ 6,~21 $ になるという。
(1) $ x $ の値の範囲を求めよ。 (2) $ y $ の値の範囲を求めよ。
解答は右画像。解説動画はこちら → 設問 (1)、設問 (2)
自分でも驚きましたが、どう考えていいやら全く分からず…始めは頭が真っ白でした。
しばらくして、設問の (1) は何とか分かってきましたが、設問 (2) に付いてはね…本当にお手上げ。( ^^;
一応自分なりに答は出してみたものの、予想通り間違った答でした。_| ̄|○
この設問 (2) に対して正しい解答をするためにも、先に上げた
・不等式どうしを引き算してはいけないのは何故か?
その理由をちゃんと理解しなければなりませんでした。
青チャート式数学の解説動画にも、この理由には触れておらずただ単に
「引き算をする、各辺を引くと言うのは上手く行かないんです。(中略) 基本の考えとして各辺で足し算する」
と、コメントを付けているのみです。
ここを深堀すると、ちょっと解説が長くなってしまうからでしょうね。
と言うことで、自分なりに納得するためには、シンプル問題に置き換えてかんがえてみることでしょう。
こんな問題について考えてみました。
問題
$ 1 \lt x \lt 2, 4 \lt y \lt 7 $ のとき、$ x -y $ の範囲を不等式で表せ。
$ 1 \lt x \lt 2, 4 \lt y \lt 7 $ のとき、$ x -y $ の範囲を不等式で表せ。
この問題…昨日までの私の頭では、下記のような答になってしまいます。
「$ x -y $ なんだから、まず最小値は $ 1 -4 $ で $ -3 $ 。最大値は $ 2 -7 $ で $ -5 $」
つまり答は $ -3 \lt x -y \lt -7 $
これは不等号の向きからしておかしいですよね。_| ̄|○
じゃあ不等式の向きを変えれば OK かと申しますと…これも違います。
どうしてこうなっちゃうのかを考えるためには、私は下記のように数直線を描いてみた次第です。

これを眺めながらやっと腑に落ちるようになりました。
$ x -y $ について、この値の最小値が左側、そして最大値が右側にくればいいんですよね。
言いたいことは、下記の式で伝わりますかな?
最小値 $ \lt x -y \lt $ 最大値
この最小値と最大値を求めるためには、どうしたらいいでしょうか?
そう考えると見えてきますよね。
まず最小値は、$ x $ が取りうる範囲の最小値から $ y $ が取りうる範囲の最大値を引けば出てきますよね。
$ 1 -7 = -6 $
つぎに最大値は、$ x $ が取りうる範囲の最大値から $ y $ が取りうる範囲の最小値を引けば出てきます。
$ 2 -4 = -2 $
つまり答は $ -6 \lt x -y \lt -2 $
さて、こうしてみると
・最小値を計算するのに、$ x,~y $ の最小値と最大値。
・最大値を計算するのに、、$ x,~y $ の最大値と最小値。
と言った具合にややこしい思考が必要になります。
それを解消するには、青チャート式数学の解説動画でコメントしているように、
「各辺で足し算できるような形にして計算する」
なんですよね。
$ y $ の方の範囲を各辺で足し算できるようにするためには、$ -1 $ を範囲指定の式に掛けてやればいいですよね。
$ -7 \lt -y \lt -4 $
こうしてやれば、$ x -y $ の範囲は、
$ ~1 \lt ~~x \lt ~2 $
$~+ -7 \lt -y \lt -4 $
-----------------------
$ -6 \lt x -y \lt -2 $
では今日も1日の習慣を始めてます。小さな一歩・挑戦を試みています。
(休日は充実した日々によって輝きますよね)
閲覧(275)
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |





 前の日記
前の日記



