皆さん こんにちは、時空 解です。

２日前には、解説動画を視聴しても腑に落ちなかった重要例題４３。
 
何が腑に落ちないかと申しますと、それはズバリ！　青チャートの解答で示される漸化式です。

　　　$ a_n =a_{n -1} +a_{n -2} ( n \geqq 3 ) $

解答には下記のように解説されていますが…



問題に初めて取り組んだ２日前には、上記の解説を見ても全く理解できませんでした。( ^^;

でもそれからずっと、頭の中で時折この問題のことを想起していましてね。
それで    思い当たったことが有ります。

それは
「ハノイの塔の問題の解法に似てるかな？」
と言うことです。

ハノイの塔に付いては、下記のブログの中でご紹介している動画が参考になります。
・今日から再び漸化式の学習。漸化式が利用できるいい例を発見、ハノイの塔

紹介してある動画では、ハノイの塔を解くための漸化式の立て方が解説されます。

まず、ハノイの塔の問題とは。
この「何手掛かるのか？」と言う問いに対して漸化式を使っていいます。

今回の重要例題４３にも似た応用が出来ることに気が付きました。

まずは
"ハノイの塔は最短で何手かかるか？"
そのポイントを下記の画像で示します。


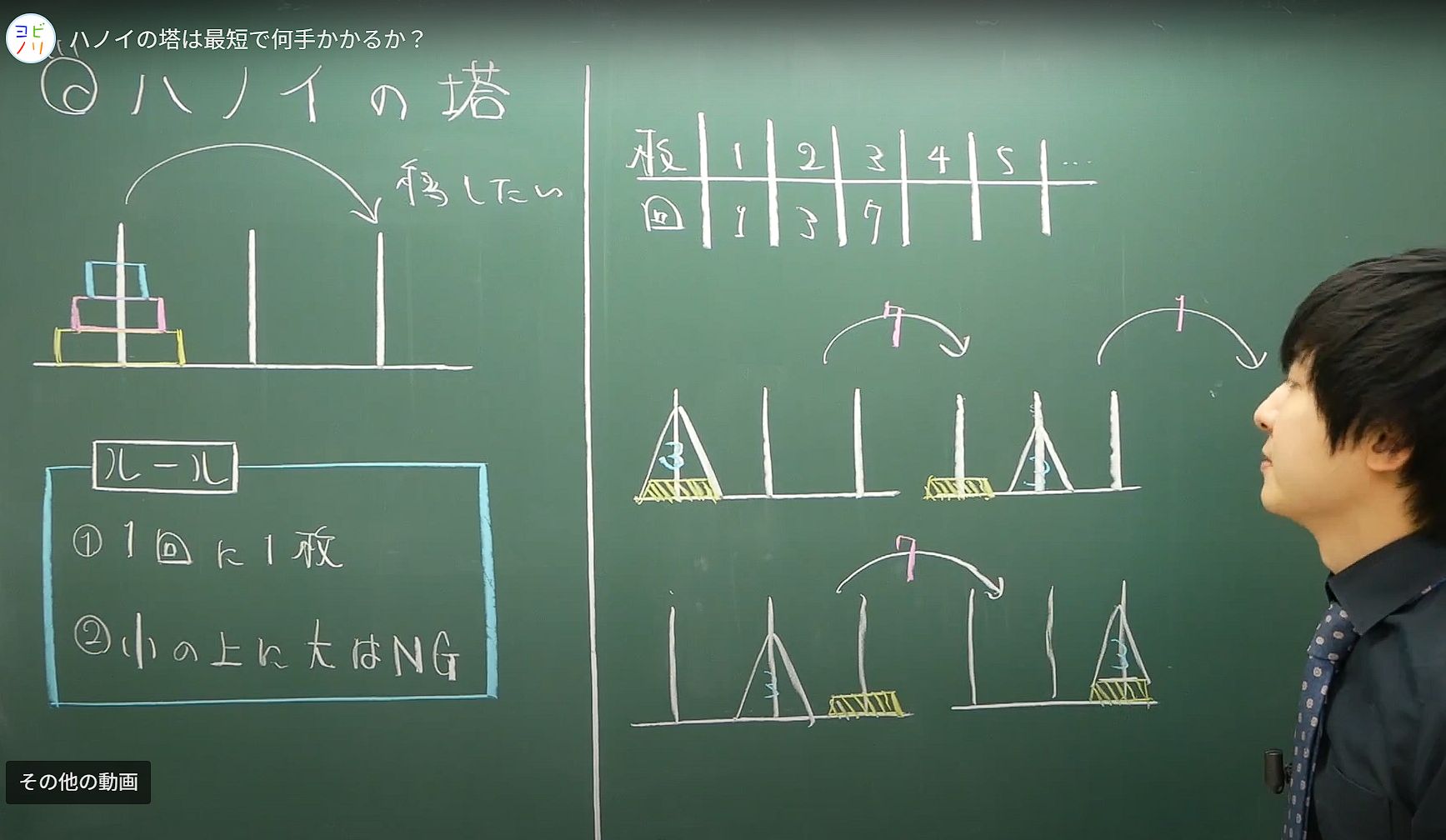
左図は
「３輪 積まれているハノイの塔と４輪 積まれているハノイの塔」
に付いて考えています。

３輪のハノイの塔を移動するには７手。
だから４輪のハノイの塔は、３輪の下にもう１輪あることに注目。
上の３輪を全て移動して初めて１番したの輪を移せます。
そしたらまた、３輪の輪を、今移動したばかりの輪に左移す。これに７手。
つまり、
(４輪のハノイの塔は ３輪のハノイの塔の７手 + １番下の輪１手 + ３輪のハノイの塔の７手) = ( $ a_4 = a_3 +  1 + a_3 $ ) = ( $ a_{n +1} = 2a_n + 1 $ )

この発想をもとにすると、今回の重要例題４３の漸化式も理解出来たんです。

どうでしょうか？　皆さんもピンと来ましたでしょうか？

重要例題４３の漸化式は
(a) $ n -1 $ 段まで来たら後は $ n $ 段に上る方法は "１段上がる" の１つしかない。
(b) $ n -2 $ 段まで来た状態では、次に $ n $ 段に上る方法として "１段上がる" と "２段上がる" の２つあるが "１段上がる" のは上記の (a) に他ならない。従って、残りは "２段上がる" の１つしかない。
(a)、(b) より、$ a_n = a_{n -1} + a_{n- 2} $

まぁこの説明よりも青チャートの解説の方がやっぱりシンプルですけどね。
自分なりに解釈してみて、改めて青チャートの解説を見ると納得ですね…。

では今日も１日の習慣を始めてます。小さな一歩・挑戦を試みています。
(休日は充実した日々によって輝きますよね)