時空 解 さんの日記
2025
8月
2
(土)
16:47
本文
皆さん こんにちは、時空 解です。
今日は問題2を解き直してみます。
(図が雑ですみません…)
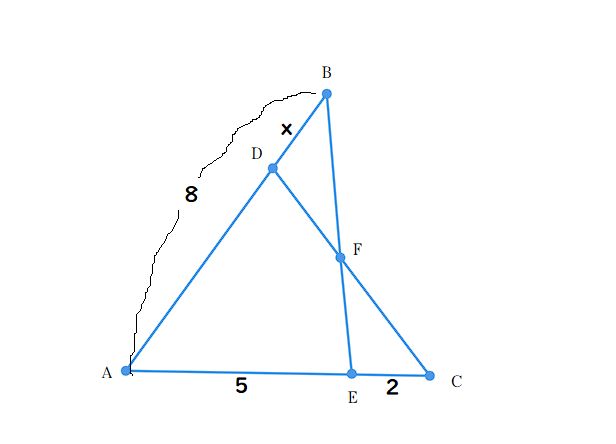
この問題は添えられている図から
「ああ、メネラウスの定理を使うやつだな」
と、直ぐに分かりますよね。
でもね。分かったところで…難しいんですよね。( ^^;
図に記されている頂点 $ A,~~B,~~C $ の位置が、メネラウスの定理の公式とそれと同じではないからね。
頭が混乱する。_| ̄|○
まぁメネラウスは「頂 → 分 → 頂 で一筆書き」と言うですから、何とか解けそうでしたけどね。
と言うことでまずは設問 (1) 。
これはメネラウスの定理は必要ありませんでしたね。
まぁこれは解説する必要もないでしょが、$ D $ と $ E $ が円に接しているのだから、点 $ A $ から接している円の中心に線を引いてみてください。
線分 $ AD $ が線分 $ AE $ と同じ長さになることは明白です。ですから $ x = 8 -5 $ となります。
次に設問 (2) ですが、これがメネラウスの定理を使って解く設問ですね。
ポイントは「$ BE $ が $ 7:4 $」と言う問題文の表現のところでしょう。
これは言い換えると $ BF:FE = 7:4 $ と言うこと。
もしも「$ EB $ が $ 7:4 $」と言う表現ならば $ BF:FE = 4:7 $ と反対に考えないとね。
この点に気を付ければ、後はメネラウスの定理を利用すれば $ x $ の式を立てることができます。
さて、設問 (3) に付いて…個人的には時間が無くて解けなかった設問でした。
ですが、これは方べきの定理を使えば解ける問題ですね。
冷静な頭ならば解けたはずの問題だったと思います。( ^^;
やっぱり試験中は緊張しているものですね。
$ \triangle ABC \unicode[sans-serif]{x223D} \triangle AED $
上記の相似関係に気が付けなかったのですから。
これで合っていると思います。
ここは $ 0.6 $ 点貰えるかな…。
では今日も1日の習慣を始めてます。小さな一歩・挑戦を試みています。
(休日は充実した日々によって輝きますよね)
今日は問題2を解き直してみます。
(図が雑ですみません…)

第444回数学検定2級2次 問題2 (選択)
右の図のように、線分 $ AB $ 上に点 $ D $ 、線分 $ AC $ 上に点 $ E $ をとり、直線 $ BE $ と $ CD $ の交点を $ F $ とします。
$ AB = 8 $ 、$ AE = 5 $ 、$ CE = 2 $ 、$ BD = x (0 \lt x \lt 8) $ のとき、次の問いに答えなさい。
(1) ある1つの円が直線 $ AB $ と $ AC $ にそれぞれ点 $ D,~~E $ で接するとき、$ x $ の値を求めなさい。この問題は解法の過程を記述せずに、答えだけを書いてください。
(2) 点 $ F $ が線分 $ BE $ を $ 7:4 $ に内分するとき、$ x $ の値を求めなさい。
(3) 4点 $ B,~~C,~~D,~~E $ が同一円周上にあるとき、$ x $ の値を求めなさい。
右の図のように、線分 $ AB $ 上に点 $ D $ 、線分 $ AC $ 上に点 $ E $ をとり、直線 $ BE $ と $ CD $ の交点を $ F $ とします。
$ AB = 8 $ 、$ AE = 5 $ 、$ CE = 2 $ 、$ BD = x (0 \lt x \lt 8) $ のとき、次の問いに答えなさい。
(1) ある1つの円が直線 $ AB $ と $ AC $ にそれぞれ点 $ D,~~E $ で接するとき、$ x $ の値を求めなさい。この問題は解法の過程を記述せずに、答えだけを書いてください。
(2) 点 $ F $ が線分 $ BE $ を $ 7:4 $ に内分するとき、$ x $ の値を求めなさい。
(3) 4点 $ B,~~C,~~D,~~E $ が同一円周上にあるとき、$ x $ の値を求めなさい。
この問題は添えられている図から
「ああ、メネラウスの定理を使うやつだな」
と、直ぐに分かりますよね。
でもね。分かったところで…難しいんですよね。( ^^;
図に記されている頂点 $ A,~~B,~~C $ の位置が、メネラウスの定理の公式とそれと同じではないからね。
頭が混乱する。_| ̄|○
まぁメネラウスは「頂 → 分 → 頂 で一筆書き」と言うですから、何とか解けそうでしたけどね。
と言うことでまずは設問 (1) 。
これはメネラウスの定理は必要ありませんでしたね。
設問 (1) の私なりの解答
$ \underline { Ans: x = 3 } $
$ \underline { Ans: x = 3 } $
まぁこれは解説する必要もないでしょが、$ D $ と $ E $ が円に接しているのだから、点 $ A $ から接している円の中心に線を引いてみてください。
線分 $ AD $ が線分 $ AE $ と同じ長さになることは明白です。ですから $ x = 8 -5 $ となります。
次に設問 (2) ですが、これがメネラウスの定理を使って解く設問ですね。
ポイントは「$ BE $ が $ 7:4 $」と言う問題文の表現のところでしょう。
これは言い換えると $ BF:FE = 7:4 $ と言うこと。
もしも「$ EB $ が $ 7:4 $」と言う表現ならば $ BF:FE = 4:7 $ と反対に考えないとね。
この点に気を付ければ、後はメネラウスの定理を利用すれば $ x $ の式を立てることができます。
設問 (2) の私なりの解答
メネラウスの定理より
$ \displaystyle \frac{AC}{CE} \cdot \frac{EF}{FB} \cdot \frac{BD}{DA} = \frac{7}{2} \cdot \frac{4}{7} \cdot \frac{x}{8-x} = 1 $
$ x $ に付いて解くと
$ x = \displaystyle \frac{ 8 }{ 3 } $
$ \underline { Ans: \displaystyle \frac{ 8 }{ 3 } } $
メネラウスの定理より
$ \displaystyle \frac{AC}{CE} \cdot \frac{EF}{FB} \cdot \frac{BD}{DA} = \frac{7}{2} \cdot \frac{4}{7} \cdot \frac{x}{8-x} = 1 $
$ x $ に付いて解くと
$ x = \displaystyle \frac{ 8 }{ 3 } $
$ \underline { Ans: \displaystyle \frac{ 8 }{ 3 } } $
さて、設問 (3) に付いて…個人的には時間が無くて解けなかった設問でした。
ですが、これは方べきの定理を使えば解ける問題ですね。
冷静な頭ならば解けたはずの問題だったと思います。( ^^;
やっぱり試験中は緊張しているものですね。
$ \triangle ABC \unicode[sans-serif]{x223D} \triangle AED $
上記の相似関係に気が付けなかったのですから。
設問 (3) の私なりの解答
方べきの定理より $ \triangle ABC \unicode[sans-serif]{x223D} \triangle AED $ である。
$ \therefore AE \cdot AC = AD \cdot AB $
$ 5 \cdot 7 = (8-x) \cdot 8 $
$ x = \displaystyle \frac{ 29 }{ 8 } $
$ \underline { Ans: x = \displaystyle \frac{ 29 }{ 8 } } $
方べきの定理より $ \triangle ABC \unicode[sans-serif]{x223D} \triangle AED $ である。
$ \therefore AE \cdot AC = AD \cdot AB $
$ 5 \cdot 7 = (8-x) \cdot 8 $
$ x = \displaystyle \frac{ 29 }{ 8 } $
$ \underline { Ans: x = \displaystyle \frac{ 29 }{ 8 } } $
これで合っていると思います。
ここは $ 0.6 $ 点貰えるかな…。
では今日も1日の習慣を始めてます。小さな一歩・挑戦を試みています。
(休日は充実した日々によって輝きますよね)
閲覧(2369)
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |





 前の日記
前の日記



