皆さん こんにちは、時空 解です。

今日は表題のとおり、数列の漸化式問題、重要例題５３を学習していました。
(問題と解答は右画像参照)

…うーむ…青チャート式数学の解答を見てみると、設問 (1),(2) はとても見事な樹形図を描いています。
(設問 (3) はまた別途)

でもね。なんだか設問 (2) の考え方は、どうにも抜けがあるように想えてなりません。
ここが場合の数・確率に関して自身のセンスがないところ何でしょうが…。＿|￣|○

本当に設問 (2) を解くための考え方が下記のような物でいいのでしょうか？


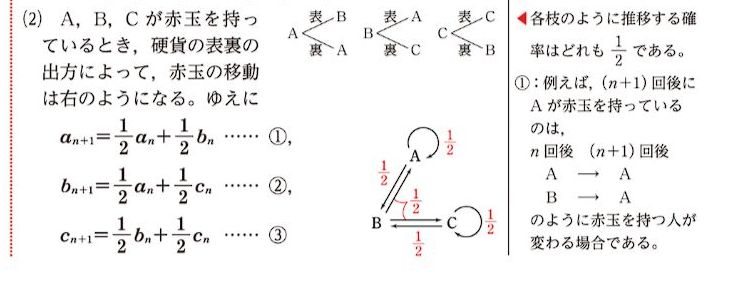
うーむ…疑問です。( ^^;

この考え方で、最終的に赤玉である確率を計算していますが…。
実際にこの一般項の式を計算して、現実と一致するのか確認したい気分です。

…それとも皆さんはどう思われますか？
青チャート式数学の解答を見て
「なるほど！」
と納得出来てますか？

…まぁ何となく正しいような気もしますが…納得できる方がうらやましいです。

では今日も１日の習慣を始めてます。小さな一歩・挑戦を試みています。
(休日は充実した日々によって輝きますよね)