皆さん こんにちは、時空 解です。

まずは、昨日ブログの投稿をサボってすみませんでした。m( _ _;)m
疲れてしまっていまして…バタンキューだったので。
(最近、水泳を頑張っている最中で、1300m を無理して泳いでいます)

ところで、どうしても納得のいかなかった問題があったんです。
まずはその問題とその答を下記と画像に示します。
 
この問題は相加平均と相乗平均の大小関係を利用して証明する問題なんです。
でも、下記のように自分で問題を解いてみて、さて？　どうして自分の解き方だと間違えるんでしょうねぇ…。
 

この問題を初めて見て解いた時は、上記のように解いたんです。( ^^;
でも、考えてみれば $ x $ は $ x \gt -1 $ なんですからね。$ x \neq -1 $ です。
それに
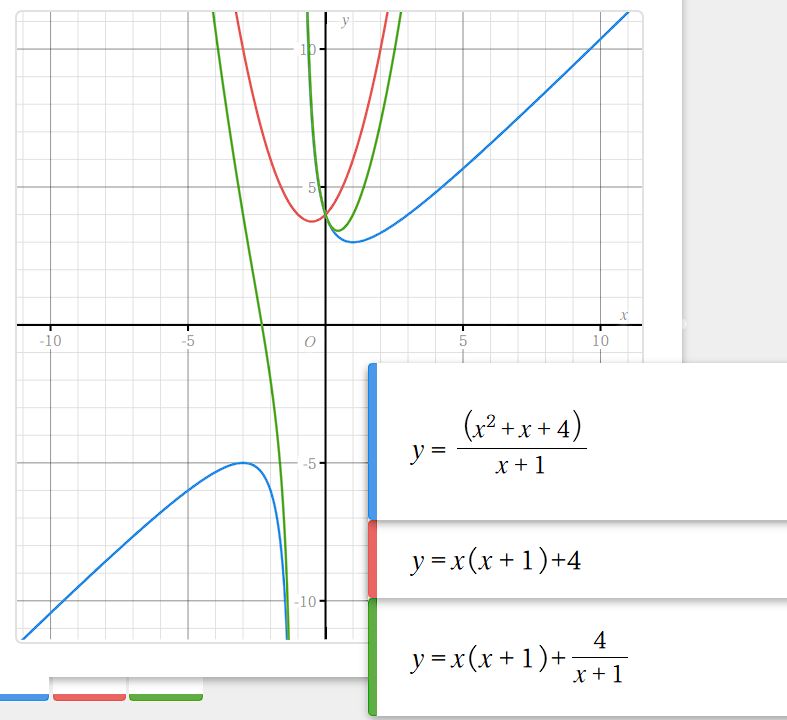
$ x = -0.99 $ として計算してみても $ (x +1) \cdot x $ 余り $ 4 $ に代入すると $ 3.9901 $ となって、とても $ 3 $ には近付きません。
(下記グラフ参照)



例えば $ 10.1 \div 2 $ を計算すると $ 5.05 $ ですよね。
または、商は整数とすると $ 5 $ 余り $ 0.1 $ ですよね。ですから、$ 10.1 $ は $ 2 × 5 $ に余りを足して $ 2 × 5 +0.1 = 10.1 $ …こうなるんでね。なんだか正しい気がしてきます…

うーむ…こんなことを考えていると、自分の解答のどこが間違っているのか分からなくなってきます。
まぁ高次方程式の余りを単純に足し込んでいるところがダメなんですけどね。

でも、悩みました…＿|￣|○

結局、相加平均と相乗平均 $ a +b \geqq 2 \sqrt{ a +b } $ で大切なのは $ a \gt 0 ,~ b \gt 0 $ と言う条件。
なので、問題の与式 $ \displaystyle \frac{ x^2 +x +4 }{ x +1 } $ を変形するに当たって注意する点は
$ x^2 $ となる項を作らず、しかも $ a $ と $ b $ 両方に対応させる項は $ x $ を含む項２つに分けて変形。
そう変形した式に付いて相加平均、相乗平均を利用するところでしょう。

そんな解釈でこの問題を理解しました。

では今日も１日の習慣を始めてます。小さな一歩・挑戦を試みています。
(休日は充実した日々によって輝きますよね)