皆さん こんにちは、時空 解です。

今日は表題に書いたとおり、数学検定の受検日です。

でもね。
今日の検定で準１級に合格出来るとは思っていないんですよね。なにせ勉強不足ですから…。
まぁ受検には出掛けますけどね。

とにかく今日の朝は下記の問題を丁寧に学習していました。自分が苦手な "場合の数" からの問題です。
 

上記のシンプルで基本的な問題を解くための考え方を、いまだにシッカリと理解・納得できてなかった私です。
でも今日でやっと納得した次第です。

上記の問題を本当にちゃんと理解するために、まずは解説動画をキチンと視聴しました。
それで思ったことですが…今まで私は樹形図と言うものをバカにしてたんです。( ^^;

樹形図を自らキチンと書こうなんて、思ってなかったんですね。

もちろん樹形図で解いている問題の解答は目にしてますが
「あ、こう書けばいいのね」
と、見ただけで実際に自分で書いてみて確認したことは皆無だったんでしょう…きっと。＿|￣|○

今回の基本例題８も
「あ、この問題か…」
と、分かっているつもりが、いざ解こうとすると
「あれっ？…どうだっけ、約数の数は指数部の数字を掛け合わせるだけだっけ、それとも、それぞれに１を足して掛け合わせる？」
と、迷ってしまうんです。

約数の合計数に至っては
「…どうやるんだっけ？」
と、解法が分からなく成っちゃっていたんです。

ダメだねぇ。
自分の学習方法はまだまだいい加減な感じです。
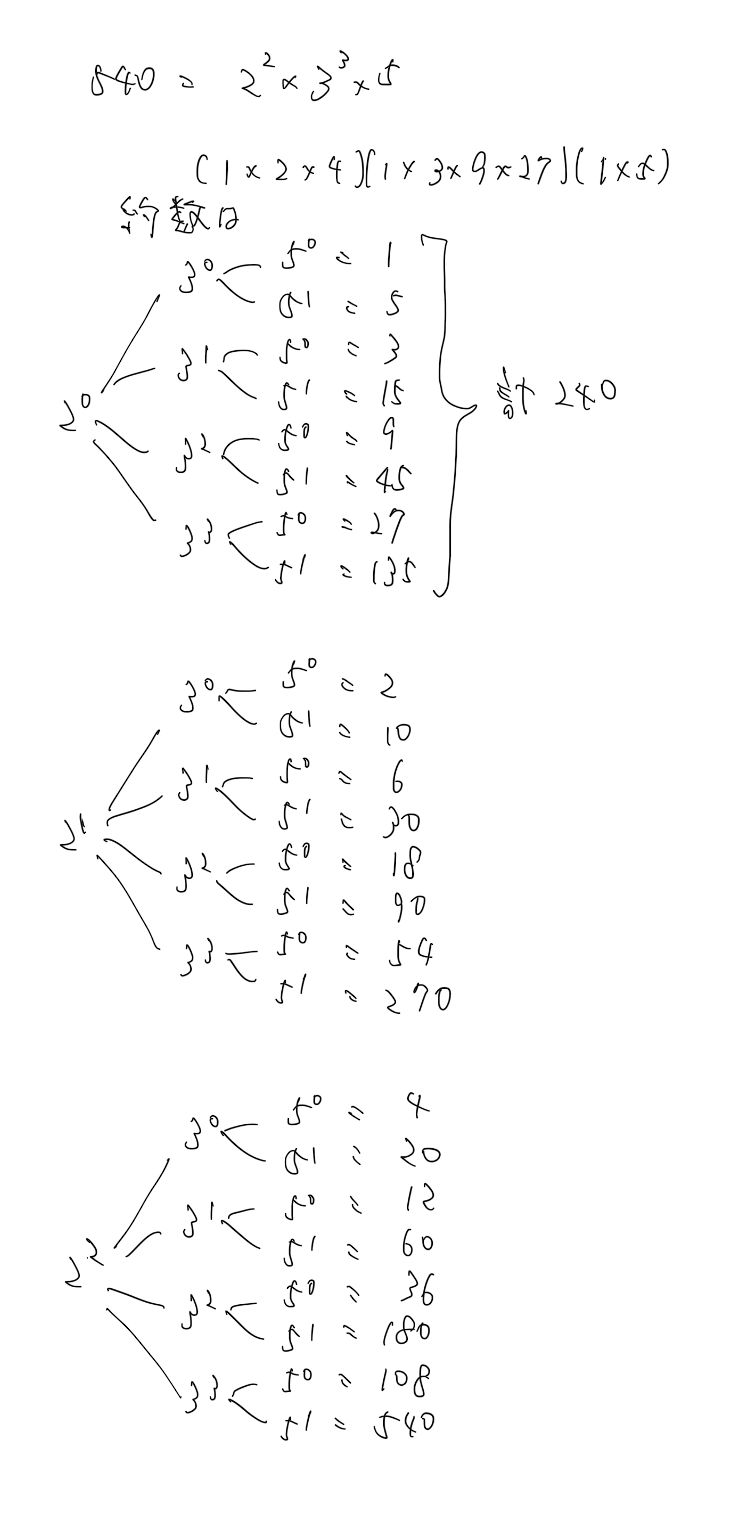
今回は右画像に示したように、ちゃんと樹形図を書き出して、約数の合計数も計算してみました。

樹形図を書いて確信が持てたことですが、本当に重複なく約数が書き並ぶんですね。(当たり前だけど…納得！)
それに、約数の合計数もちゃんと答と同じ値になります…。(これはやってみて、確信できた)

こんな私でも、今日は準１級を受検しに行ってきますね。( ^^;

では今日も１日の習慣を始めてます。小さな一歩・挑戦を試みています。
(休日は充実した日々によって輝きますよね)