問題１
$ k $ を定数とします。$ xy $ 平面上の円 $ \left( x +  \displaystyle {\frac{ 3 }{ 2 }} k \right)^2 +(y -2k)^2 = \displaystyle \frac{ 25 }{ 4 } k^2 +4 $ は、$ k $ の値によらず２つの定点を通ります。
その２点の座標を求めなさい。

模範解答による答 $ (x,~y) = \left(  \displaystyle { \pm \frac{ 8 }{ 5 },~\pm \frac{ 6 }{ 5 }} \right) $

$ k = -2 $ を与式に代入して整理すると
　　　$ \left( x -3 \right)^2 + \left( y +4 \right)^2 = 29 $
展開すると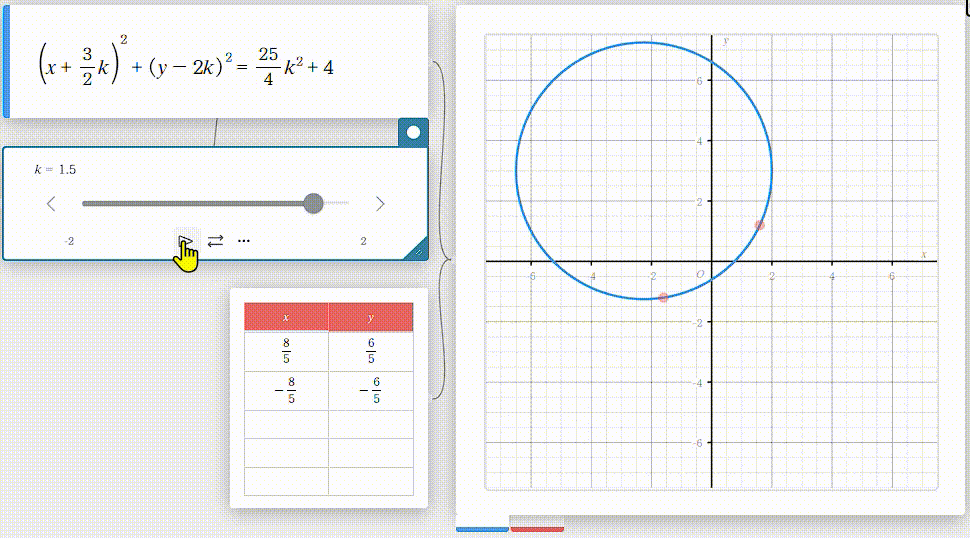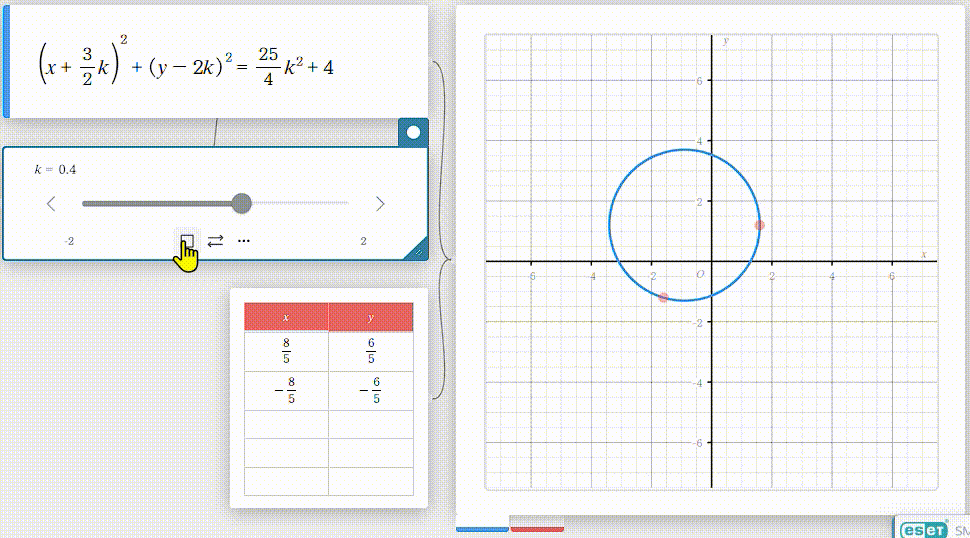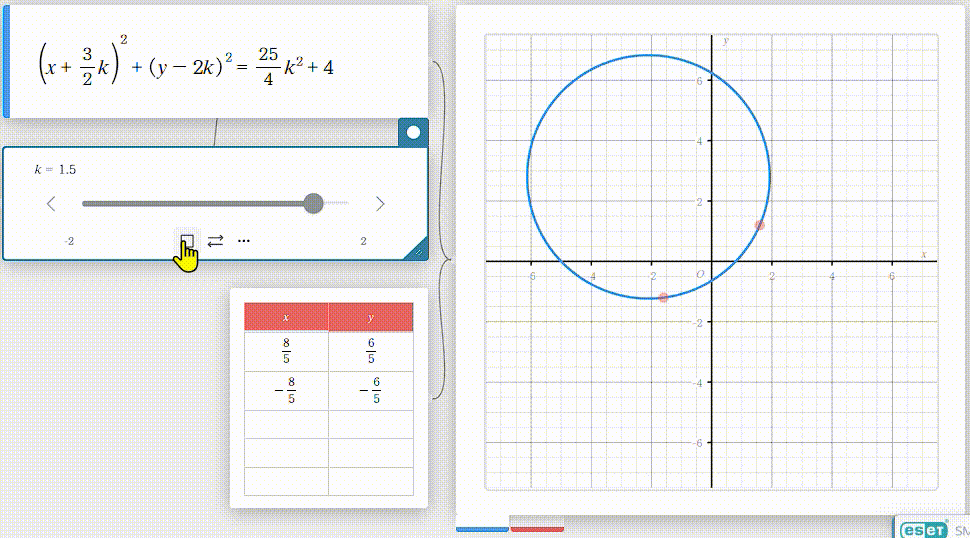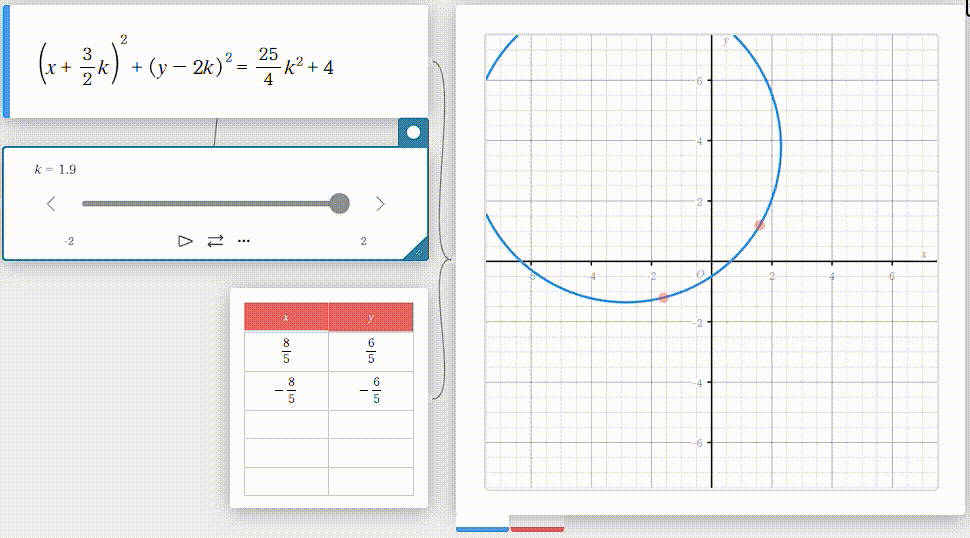
　　　$ x^2 +6x +9 +y^2 -8y +16 = 29 $　　　(a)

同様に $ k = 2 $ を代入して整理すると
　　　$ \left( x +3 \right)^2 + \left( y -4 \right)^2 = 29 $
展開すると
　　　$ x^2 -6x +9 +y^2 +8y +16 = 29 $　　　(b)

$ k = 0 $ の時は
　　　$ x^2 +y^2 = 4 $　　　　　　(c)

(a), (b), (c) より $ x,~y $ を求める。
(a) - (b) より
　　　$ 12x -16y = 0 $
　　　　$ y = \displaystyle \frac{ 3 }{ 4 } x $
(c) に上記の $ y $ を代入して
　　　$ x^2 + \left(  \displaystyle {\frac{ 3 }{ 4 } x } \right)^2 = 4 $

これより $ x = \pm \displaystyle \frac{ 8 }{ 5 } $　　また $ y = \pm \displaystyle \frac{ 6 }{ 5 } $