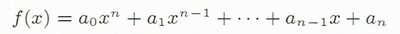時空 解 さんの日記
2017
4月
19
(水)
08:29
前の日記
本文
皆さん、おはようございます。 時空 解です。
数学検定３級の検定が終了したばかりですが昨日、準２級の数学検定に向けて勉強を始めました。まぁ青チャートの数学I+A を始めたんですけどね。
準２級用の要点整理と過去問題集も昨日の内にアマゾンから届きました。( 早いですよね ) これで次回の検定日に向けて勉強を進めるのみです。
しかし思うようには進められないものですね。この青チャートの数学I+A には全部で４３の節があるんですが、次回の数学検定日は７月２３日。ですので準備出来る期間が約９０日間となります。期間９０日を４３節で割ると、約２日間ですので、一つの節２日で終えて行かないといけません。しかし…。昨日は１０ページから２３ページ、整式の加法・減法・乗法と言う節を一通り終わらせる予定でしたが、"整式" の説明を読んでいて時間を取ってしまいました。
青チャートの１０ページに整式の説明が載っているのですが、これって本当に正しいの？
数学検定３級の検定が終了したばかりですが昨日、準２級の数学検定に向けて勉強を始めました。まぁ青チャートの数学I+A を始めたんですけどね。準２級用の要点整理と過去問題集も昨日の内にアマゾンから届きました。( 早いですよね ) これで次回の検定日に向けて勉強を進めるのみです。
しかし思うようには進められないものですね。この青チャートの数学I+A には全部で４３の節があるんですが、次回の数学検定日は７月２３日。ですので準備出来る期間が約９０日間となります。期間９０日を４３節で割ると、約２日間ですので、一つの節２日で終えて行かないといけません。しかし…。昨日は１０ページから２３ページ、整式の加法・減法・乗法と言う節を一通り終わらせる予定でしたが、"整式" の説明を読んでいて時間を取ってしまいました。
青チャートの１０ページに整式の説明が載っているのですが、これって本当に正しいの？
上記の画像の左に整式の例が挙げられていますが、右側には反例も３つ挙げられています。「例えば(1)、(2)、(3) などは整式でない」と書かれています。
整式の定義は、この青チャートに下記のように説明されています。
この定義から、整式の反例として挙げられている数式 (1)、(2)、(3) がどうして整式ではないのか、理解に苦しみました。
同じような疑問をもった方もいるようで、YAHOO! 知恵袋に投稿されています。
・高校数学（単項式の定義）について，質問です。
同じような疑問をもった方もいるようで、YAHOO! 知恵袋に投稿されています。
・高校数学（単項式の定義）について，質問です。
この知恵袋の説明を見てもなんとも理解できません。多項式？非負数でない整数 n ？
たかが整式の定義、しかし難航しました。
そこで、最近購入したばかりの「岩波 数学入門辞典」を早速使ってみました。
これで "整式" を引いてみると "多項式" と書かれています。
"多項式" を引いてみて下記のような記述があります。
うーむ、これらから見て、下記の３つ数式がどうして整式ではないのか、と言う理由が以下のような理由だと結論しました。
たかが整式の定義、しかし難航しました。
そこで、最近購入したばかりの「岩波 数学入門辞典」を早速使ってみました。これで "整式" を引いてみると "多項式" と書かれています。
"多項式" を引いてみて下記のような記述があります。
うーむ、これらから見て、下記の３つ数式がどうして整式ではないのか、と言う理由が以下のような理由だと結論しました。
( あくまでも私の解釈ですが… )
(1) の 1/( x + 1) は 「 ( x + 1 )のマイナス１乗」となり、次数 n が負の整数となるので、非負整数(掛け合わせた文字の数)と言う定義に反する。
(2) の x + 3/x も 3/x が 「 3 掛ける ｘのマイナス１乗」となり、次数 n が負の整数となるので、非負整数(掛け合わせた文字の数)と言う定義に反する。
(3) はルート x が 1/2 乗なので、明らかに次数 n が整数ではない。
(1) の 1/( x + 1) は 「 ( x + 1 )のマイナス１乗」となり、次数 n が負の整数となるので、非負整数(掛け合わせた文字の数)と言う定義に反する。
(2) の x + 3/x も 3/x が 「 3 掛ける ｘのマイナス１乗」となり、次数 n が負の整数となるので、非負整数(掛け合わせた文字の数)と言う定義に反する。
(3) はルート x が 1/2 乗なので、明らかに次数 n が整数ではない。
さて、青チャートには次数の説明が "掛け合わせた文字の数" と説明されています。ここから推論すると確かに多項式とみた場合、次数 n は非負整数 と言う事になりますが…。
しかし、納得がいかないのは「数学入門辞典」の説明です。多項式であるというのは良しとして、どうして多項式の説明のなかに「 n は非負整数」と書かれていないのでしょうか？多項式の説明文の最後にも注意書きとして記されてもいませんし、辞典の先頭ページにある "凡例" にも n の使い方は説明されていません。
しかし、納得がいかないのは「数学入門辞典」の説明です。多項式であるというのは良しとして、どうして多項式の説明のなかに「 n は非負整数」と書かれていないのでしょうか？多項式の説明文の最後にも注意書きとして記されてもいませんし、辞典の先頭ページにある "凡例" にも n の使い方は説明されていません。
せっかく高いお金を払って買ったのにこの辞書、役に立つのかなぁ…。
そんな疑問を抱きながら、午前中が過ぎてしまいました。
そんな疑問を抱きながら、午前中が過ぎてしまいました。
でもね。よくよく多項式の式を見てみて思いました。
n は a の下付き文字と x の次数の両方に共通して使われています。そして a の添え字としては整数のゼロから n 番目と言う形で使用されているのです。これから見て、n は非負整数と言う事を言わぬもがな、と言う事なのでしょうかね？
やれやれ、２日間で青チャートの１節を終わらせる事が本当に出来るのでしょうか？昨日の苦労を想うと無理な気がしますが…。
しかしそれをやれるように対策を打つ。と言う事が必要な事なのですかね？
しかしそれをやれるように対策を打つ。と言う事が必要な事なのですかね？
本当は XOOS Cube Legacy とか ラテフと言う数式文書作成ソフト とかの勉強もしたいんです。特に数式文書作成ソフト、ラテフは学びたいのです。
何と言っても今日のブログのように書籍の部分コピー掲載は抵抗があります。著作権法上どう扱われるのか不安です。うーむ、数学の学習がもっとスイスイ出来る方法、ないかなぁ…。
時間の使い方も考えないとなぁ…。
何と言っても今日のブログのように書籍の部分コピー掲載は抵抗があります。著作権法上どう扱われるのか不安です。うーむ、数学の学習がもっとスイスイ出来る方法、ないかなぁ…。
時間の使い方も考えないとなぁ…。
ま、とにかく今は出来るスピードで進めるしかありません。効率アップ方法はまた別の機会。
応援してね。
千里の道も一歩から。そしてその道は登り坂です。
(ポチッとブログ村のバナーをクリックしてね）
にほんブログ村
「新・良い習慣化計画」
朝は七時に起きれるようになりました。
ブログも毎日更新できてます。
夜はキッカリ１１時に寝ます。
午前中はブログと勉強のみで良し。
目をいたわります。
休日にはブログ・勉強以外の事も一つやります。
勉強会の動画は YouTube チャンネル でご覧になれます。( 更新なし )
千里の道も一歩から。そしてその道は登り坂です。
(ポチッとブログ村のバナーをクリックしてね）
にほんブログ村
「新・良い習慣化計画」
朝は七時に起きれるようになりました。
ブログも毎日更新できてます。
夜はキッカリ１１時に寝ます。
午前中はブログと勉強のみで良し。
目をいたわります。
休日にはブログ・勉強以外の事も一つやります。
勉強会の動画は YouTube チャンネル でご覧になれます。( 更新なし )
閲覧(9457)
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |
メインメニュー
