50代から理数を学ぶ - たすき掛けの理解に、四苦八苦。

Home > ブログ > 時空解 > 数学 > たすき掛けの理解に、四苦八苦。

時空解さんの日記

2017

5月 2

(火)

09:37

たすき掛けの理解に、四苦八苦。

前の日記次の日記

カテゴリー数学

本文

皆さん、おはようございます。時空解です。

青チャートのチャート式基礎からの数学I+A の学習を進めるのに四苦八苦しています。今日はこの参考書の p25 にまとまっている "たすき掛けを利用した因数分解" の解説についてみてみましょう。
参考書をお持ちの方は開いてみてください。
１ページにまとめられているたすき掛け、 p25 の下半分に例が載っています。この四角の１、２、３に付いてですが…

１、２次の係数は、正の数の組み合わせだけでよい。→ どうして "正の数" の "組み合わせ" だけで良いのか？
２、b, d の組み合わせ → どうして "組み合わせ" で良いのか？

特に２ですが、私は "順列" であるべきだと考えています。

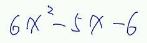
具体的に p25 ページに載っている例で考えてみましょう。説明に使われている整式は左画像に示します。
たすき掛けと言うのはその下の画像に示す通り、求める因数分解の形を縦に並べてみると分かり易いです。

係数 a,b,c,d の位置が対応しています。

さて、まずは１、２次の係数は、正の数の組み合わせだけでよい、と言う理由を考えてみたのですが、これは下記の数式を書いてみて納得が出来ます。与式は赤いアンダーライン部分のごとく因数分解できます。

赤いアンダーラインの右に書かれている因数分解は、前の ( ) と後ろの ( ) を入れ替えたものです。これで２次の係数が "組み合わせ" で良い事が理解できます。
また、赤いアンダーラインの下にマイナスを２つ掛け合わせた因数分解式を書きました。これで２次の係数は "正の数" だけを考えても良い事が理解できます。負の数を考えなくても、後の b, d の ± を考慮する事で吸収できます。

分からないのは b, d がどうして "組み合わせ" で良いのか、です。a, c と b, d の関係を考え合わせると、私は "順列" で考える必要があると思っています。下記のを見てみてください。赤のアンダーラインの部分が食い違うのが分かりますよね。

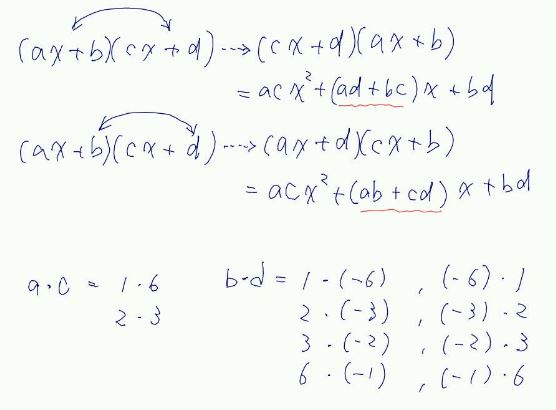
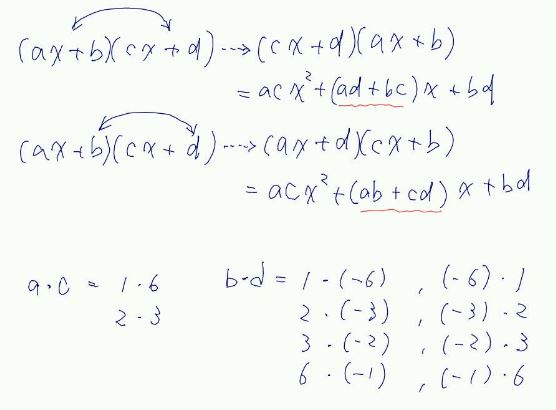
昨日はここで疲れてしまいました。と言うよりは、上記の a, c と b, d からすべてのたすき掛けを書き出すと１６ある訳ですが、そうしたところで問題が解決しそうにないと思えて疲れてしまいました。

でも、今日はこの続きから始めたいと思います。
では１日を始めます。

応援してね。
千里の道も一歩から。そしてその道は登り坂です。
(ポチッとブログ村のバナーをクリックしてね）

「新・良い習慣化計画」
　　　朝は七時に起きれるようになりました。
　　　ブログも毎日更新できてます。
　　　夜はキッカリ１１時に寝ます。
　　　午前中はブログと勉強のみで良し。
　　　目をいたわります。
　　　一日２０分はそろばんをします。
　　　休日にはブログ・勉強以外の事も一つやります。

勉強会の動画は YouTube チャンネルでご覧になれます。( 更新なし )

閲覧(5652)

コメントを書く
コメントを書くにはログインが必要です。