50代から理数を学ぶ - 因数分解のための公式、何か意味があるのか？

Home > ブログ > 時空解 > 数学 > 因数分解のための公式、何か意味があるのか？

時空解さんの日記

2017

5月 20

(土)

08:44

因数分解のための公式、何か意味があるのか？

前の日記次の日記

カテゴリー数学

本文

皆さん、おはようございます。時空解です。

昨日もチャート式基礎からの数学I+A の因数分解の節を学習して悩んでしまいました。
「この式は公式として覚えておくと便利です」と名打った式がありますが、それってどう思いますか？みなさん。

例えばこんな公式。

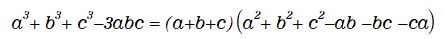
この公式と、例えば三平方の定理 ( ピタゴラスの定理 ) を想い起してもらえばいいとおもいますが…。

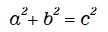
三平方の定理の方は三角形と密接な関係もあって、自然界の不思議を含んでいるようで意味を感じます。当然と言えば当然ですけどね。「因数分解をするための公式と三平方の定理は比較する式じゃないよ」と皆さんにお叱りを受けそうですが、その辺はご勘弁を。ここでは自分が言いたい事を言うためのたとえです。

因数分解をするための公式は、例えるならサイコロを１０個振った時に出る目が全てそろった、と言ったたぐいでしょうか。順列的な確率から言えば、全ての目の出方の重みは同じなのですが、１０個ともオール１の方が、１４２１６３３２１４などとバラバラに目が出た時よりも特殊な気がします。

因数分解をするための公式って、ようするに式を変形したら印象的な文字列になっている式、と言うものだと思ったりします。自然界の奥深さなどは含んでない！とおもってしまうんですよね。だから、下記の等式が因数分解をする時に便利だから、と言われても記憶する重要性を感じないのです。

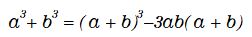
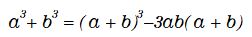
覚えられますけど、個人的には何か意味を含んだ等式であってほしいのです。

そもそも数式を変形する、と言う事は自然界の事とどう結び付くのでしょうか？

この疑問に答えてくれる書籍に、いまだ出会った事がありません。しかし２日前にご紹介した「算数・数学が得意になる本」と言う書籍の中には「つまづき」の16のパターンの中の (11),(12) に、それを匂わせる指摘が見て取れます。 "具体例の認識不足のまま学ぶ抽象概念" と "公式の適用と式変形の妥当性の吟味" と言う言い回しは気になるところです。数式の変形がどう自然界と関わってくるのか、そのヒントがこの書籍に書かれていると良いのですが…。

とにかく因数分解のための公式は覚えた方が良いと分かっているのですが、因数分解するためだけの意味では、すぐに忘れてしまいます。

式変形・・・それは "自然界のこうこうこうと言う意味" と判るはずもないものですかねぇ。

三平方の定理が何故人々の記憶に刻まれているのか？その理由は深い自然界との結びつきを感じるから、とは思っていませんよ。理由は式が簡単でしかもフェルマーの最終定理にも関わってくるので印象深い、だからでしょう。

とにかく因数分解のための公式は、定期的に見返すしかないかなぁ・・・みなさんはどうされてますか？

では今日も数学の勉強を始めます。

応援してね。
千里の道も一歩から。そしてその道は登り坂です。
(ポチッとブログ村のバナーをクリックしてね）

「新・良い習慣化計画」
　　　朝は七時に起きれるようになりました。
　　　ブログも毎日更新できてます。
　　　夜はキッカリ１１時に寝ます。
　　　午前中はブログと勉強のみで良し。
　　　目をいたわります。
　　　一日２０分はそろばんをします。
　　　休日にはブログ・勉強以外の事も一つやります。

閲覧(5441)

コメントを書く
コメントを書くにはログインが必要です。