時空 解 さんの日記
2017
7月
11
(火)
08:36
本文
みなさん、おはようございます。時空 解です。
「改訂版 チャート式 基礎からの 数学I+A」の p114 重要例題 68 (2) がやっと頭の中で整理できました。
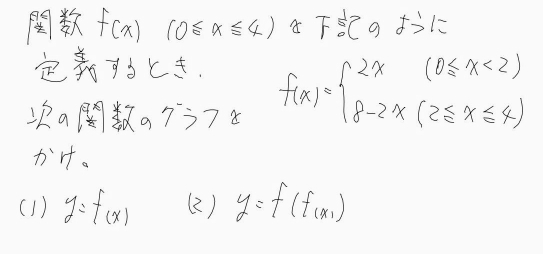
しかし、やっぱり個人的にはおかしな問題なぁと、思う次第です。
定義域の範囲を 0 ≦ x < 2 , 2 ≦ x ≦ 4 と制約していますが、この制約って何なんでしょうかね。物理学上で言ったら、どう言う意味のある制約なのか、訳が分かりません。要注意だと思うばかりです。そもそも x に対応する量と言うのは何なのか、理解に苦しみます。
x に対応させる量は何か?に付いて考える場合、慣例的には、例えば時間軸に x 軸、距離に y 軸が使われたりします。これに習って、定義域を時間と考えてこの重要例題 68 (2) の関数 f( f(x) ) を解釈してみましょう。
そうすると、入れ子のまずは内側、 f( f(x) ) の赤い部分 (お詫び:赤い部分が有りませんでした。2020-12-14 修正) を計算する時には普通に x を時間として考える事は出来ます。定義域の範囲は時間の制約として存在します。しかしこんどは外側、 f( f(x) ) に付いて考える時には、内側の計算で出した答えに対して制約を掛ける訳ですから、この場合には時間に対する制約と言うよりは別物に対する制約になるのではないでしょうか?慣例的に考えれば、距離に対しての制約になります。
「改訂版 チャート式 基礎からの 数学I+A」の p114 重要例題 68 (2) がやっと頭の中で整理できました。
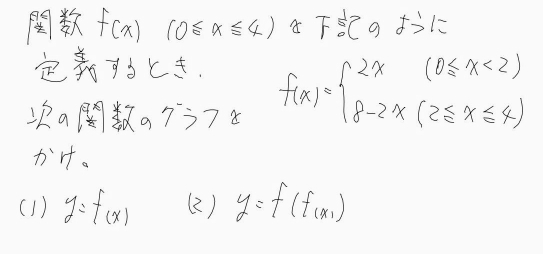
しかし、やっぱり個人的にはおかしな問題なぁと、思う次第です。
定義域の範囲を 0 ≦ x < 2 , 2 ≦ x ≦ 4 と制約していますが、この制約って何なんでしょうかね。物理学上で言ったら、どう言う意味のある制約なのか、訳が分かりません。要注意だと思うばかりです。そもそも x に対応する量と言うのは何なのか、理解に苦しみます。
x に対応させる量は何か?に付いて考える場合、慣例的には、例えば時間軸に x 軸、距離に y 軸が使われたりします。これに習って、定義域を時間と考えてこの重要例題 68 (2) の関数 f( f(x) ) を解釈してみましょう。
そうすると、入れ子のまずは内側、 f( f(x) ) の赤い部分 (お詫び:赤い部分が有りませんでした。2020-12-14 修正) を計算する時には普通に x を時間として考える事は出来ます。定義域の範囲は時間の制約として存在します。しかしこんどは外側、 f( f(x) ) に付いて考える時には、内側の計算で出した答えに対して制約を掛ける訳ですから、この場合には時間に対する制約と言うよりは別物に対する制約になるのではないでしょうか?慣例的に考えれば、距離に対しての制約になります。
これって、どう思います?
どう考えても、この問題は変な問題です。
どう考えても、この問題は変な問題です。
強いてこの問題の出題意図を想像するのならば、「関数の表記」を学ばせたいだけの問題なのかなぁ…と、そう思うしか私にはありません。f( f(x) ) と言う「表記」があって、「定義域の各一部分に対応するそれぞれの関数」をグラフにすると、こんな風になるのですよ、と言いたいのでしょうかね。
皆さんはどう思われますか?
皆さんはどう思われますか?
何はともあれ、この重要例題 68 (2) は一応は解釈できました。もしかしたら私の解釈が間違っているかも知れませんが、とりあえず頭の中に入りました。
今はまだ数学の学習しか、していないのでこんな事を考えてしまうのかも知れません。物理学の学習を始めればもしかしたら解釈が違って来る可能性もあります。その時に又、この重要例題 68 (2) を検討したいと思います。課題が出来た気分です…もしかしたら大学教授の方などから見たら、バカな課題かも知れませんが。
ただいま勉強中ですので、お許し下さいませませ。
今はまだ数学の学習しか、していないのでこんな事を考えてしまうのかも知れません。物理学の学習を始めればもしかしたら解釈が違って来る可能性もあります。その時に又、この重要例題 68 (2) を検討したいと思います。課題が出来た気分です…もしかしたら大学教授の方などから見たら、バカな課題かも知れませんが。
ただいま勉強中ですので、お許し下さいませませ。
では今日も1日を始めます。
応援してね。
千里の道も一歩から。そしてその道は登り坂です。
(ポチッとブログ村のバナーをクリックしてね)![]()
| 項目 | 昨日の実施状況 | 今日の予定 |
|---|---|---|
| ブログを更新 | 9時09分 | 8時30分 |
| そろばんの練習 | 30分 | 30分 |
| 数学の学習 | p114 | p115 ~ p125 |
| + α 学習( LaTeX2ε 、コンテンツ作成など ) | 「エディタを使う時のポイント」下書き途中 | 「エディタを使う時のポイント」下書き |
閲覧(7759)
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |





 前の日記
前の日記



