時空 解 さんの日記
2017
7月
14
(金)
08:46
本文
皆さん、おはようございます。時空 解です。
受検証が手元に届いたので、数学の学習を頑張ろうと思っているのですが、つまづいています。
「改訂版 チャート式 基礎からの 数学I+A」の p116 に説明されている <曲線の平行移動> に付いてですが、これを頭の中でどう整理していいのやら、困っています。
<曲線の平行移動> に付いては、高校時代には頭の中で納得出来ていた事を覚えています。しかし今ではちょっと不安を感じるところです。人に説明出来るようでなくては、自分自身にも、説得・納得できないのですよね。これが「歳を取る」と言う事かも知れません。
受検証が手元に届いたので、数学の学習を頑張ろうと思っているのですが、つまづいています。
「改訂版 チャート式 基礎からの 数学I+A」の p116 に説明されている <曲線の平行移動> に付いてですが、これを頭の中でどう整理していいのやら、困っています。
<曲線の平行移動> に付いては、高校時代には頭の中で納得出来ていた事を覚えています。しかし今ではちょっと不安を感じるところです。人に説明出来るようでなくては、自分自身にも、説得・納得できないのですよね。これが「歳を取る」と言う事かも知れません。
<曲線の平行移動> と言うのを簡単に説明すると、下記のようになります。
関数 y = f(x) を2次関数とすると、このグラフは放物線のグラフになります。まずこれをブラフ F とします。このグラフ F を x 方向に p 、y 方向に q 平行移動したグラフを G とします。すると、この G の方程式は、F の方程式の x を x-p, y を y-q でおき換えたものになっている。
この説明のどこに引っかかるのかと言うと
・x-p ではなくて x+p なんじゃないかなぁ…
・y-q じゃなくて y+q なのではないのかなぁ。
といった具合です。
・x-p ではなくて x+p なんじゃないかなぁ…
・y-q じゃなくて y+q なのではないのかなぁ。
といった具合です。
例えばこれを、曲線のグラフの平行移動ではなくて、直線のグラフの平行移動で考えるならば、y に付いては納得が行きます。
y = ax ( これを F ) の直線グラフと y = ax + b ( これを G ) の直線グラフの関係を考えてみて下さい。
グラフ F を y 方向に b 平行移動したものが G ですね。
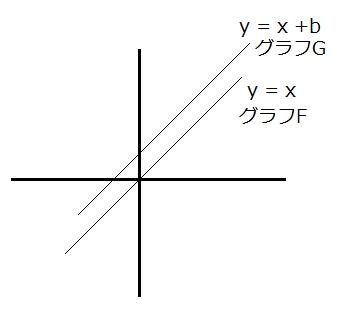
y = ax ( これを F ) の直線グラフと y = ax + b ( これを G ) の直線グラフの関係を考えてみて下さい。
グラフ F を y 方向に b 平行移動したものが G ですね。
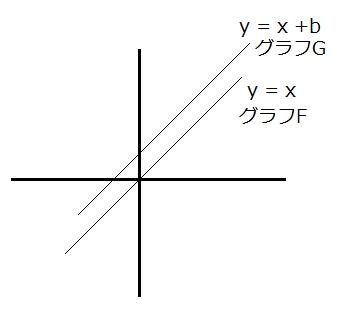
だから G の方程式は、F の方程式の y を y-b で置き換えたもの、と言われれば納得できるでしょう。
なぜならば y = ax + b を変形すると y - b = ax ですからね。
ですから、y成分 に付いては曲線の平行移動に付いても納得は出来ます。
「でも x は?」 となるとちょっと頭の中が整理付きません。説明がうまく出てこないのです。
なぜならば y = ax + b を変形すると y - b = ax ですからね。
ですから、y成分 に付いては曲線の平行移動に付いても納得は出来ます。
「でも x は?」 となるとちょっと頭の中が整理付きません。説明がうまく出てこないのです。
と言う事で、数学検定の検定日が近づていますがなかなか学習が進まないのです。
ところで…。
この <曲線の平行移動> なのですが、実は数学検定準2級のテキスト「実用数学技能検定 要点整理 準2級」の中には出てこないのですよね。
と言う事でこれに付いては今後の課題と言う事で、あまり足踏みはせずに次に進もうと思っています。
この <曲線の平行移動> なのですが、実は数学検定準2級のテキスト「実用数学技能検定 要点整理 準2級」の中には出てこないのですよね。
と言う事でこれに付いては今後の課題と言う事で、あまり足踏みはせずに次に進もうと思っています。
とにかく、今日も1日を始めます。
応援してね。
千里の道も一歩から。そしてその道は登り坂です。
(ポチッとブログ村のバナーをクリックしてね)![]()
| 項目 | 昨日の実施状況 | 今日の予定 |
|---|---|---|
| ブログを更新 | 9時36分 | 8時30分 |
| そろばんの練習 | 30分 | 30分 |
| 数学の学習 | p115 ~ p116 | p117 ~ p125 |
| + α 学習( LaTeX2ε 、コンテンツ作成など ) | 「エディタを使う時のポイント」公開できず | 「エディタを使う時のポイント」公開する |
閲覧(8246)
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |





 前の日記
前の日記



