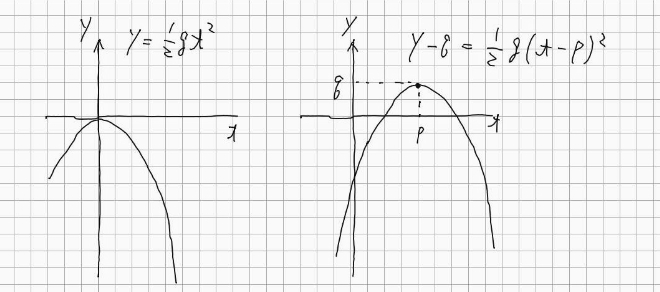時空 解 さんの日記
2017
7月
22
(土)
10:21
前の日記
本文
皆さん、おはようございます。時空 解です。
昨日は予定通り数学検定の検定会場の下見に行ってきました。前回の会場よりは小さい場所ですね。座席数からすると１２０人と言うことろです。一つのテーブルに３つ腰掛が置いてありましたが、検定当日は真ん中を使わないはずですから、受検者数は８０人と言ったところでしょう。前回の春の時の半分くらいの受検者と言う感じですかね。ビルの９階にあるホールです。エレベーターは４台ありますが、向かって右側の２つは６階止まりのエレベーターです。気を付けましょう。
昨日は予定通り数学検定の検定会場の下見に行ってきました。前回の会場よりは小さい場所ですね。座席数からすると１２０人と言うことろです。一つのテーブルに３つ腰掛が置いてありましたが、検定当日は真ん中を使わないはずですから、受検者数は８０人と言ったところでしょう。前回の春の時の半分くらいの受検者と言う感じですかね。ビルの９階にあるホールです。エレベーターは４台ありますが、向かって右側の２つは６階止まりのエレベーターです。気を付けましょう。
さて、下見から帰って来て感じたのですが、ちょっと疲れました。家を出たのが９時で帰って来たのが１０時半。たったの１時間半の外出ですが、歳ですかねぇ。疲れる何て事は考えもしなかったのですが、２次の過去問題、やる気になれませんでした。
と、言う事で少し検定からは離れて、昨日は曲線のグラフの移動に付いて考えてみました。考えてみた、と言うよりはずっと気持ちの中で引っかかっていた、というべきでしょう。チャート式の参考書で学習した数日前からの引っかかりです。
y = f(x)と言うグラフを y 方向に +p、x 方向に +q 平行移動した時に関数は
y - q = f(x-p)
で表される。
と言うやつです。
グラフを絵的にプラス方向に平行移動した時の直感と、数式 ( 符号が逆 ) が違ってくる事がシックリ来ません。
どうして y + q = f(x+p) ではないのか？
と言う疑問ですよね。
これをどう頭の中で整理するかです。私は自由落下の方程式で考えてみました。
どうして y + q = f(x+p) ではないのか？
と言う疑問ですよね。
これをどう頭の中で整理するかです。私は自由落下の方程式で考えてみました。
放物線のグラフを上に凸で書いたのは x と y との関係を落下の距離と時間の関係として示したかったからです。つまり f(x) を自由落下の方程式を例に取って考えてみましょう。そうすると放物線のグラフを平行移動すると言う事はどういう意味なのか考え易くなります。
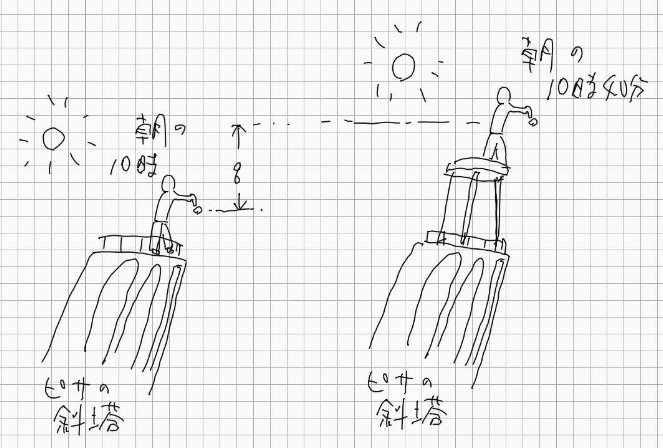まずは y 軸方向に +q するとはどういう事かと言うと、それは自由落下をさせる位置を +q すると言う事です。図で表すならば例えば高い台の上から自由落下を試みるのと一緒です。台の高さが +q ですね。次に t 軸方向に +p するとはどういう事かと言うと、これは高い台を準備してその台の上によじ登ってから自由落下を試みる事と考えられます。台を用意してよじ登るのに掛かる時間が +p と言う事ですね。
さて、手から石を離した時に、石はどんな落ち方をするでしょうか？
落とす位置によって違いがあるでしょうか？
落とす時刻によって違いがあるでしょうか？
これは分かりますよね。違いはありません。
落とす高さをグッと高くして、地球からかなり離れた高さから落とすなら、重力の掛かり方が変わりますから違いは出て来ます。でもこの場合はそんなに高い台 (+q) を想定していませんので重力変化は無いものと考えて下さいね。
それと時間に関しては全く問題はないでしょう。もっとも太陽の超新星爆発膨張時刻まで未来 (+p) の話をした場合には違ってきます。ピサの斜塔どころか地球が太陽に飲み込まれてしまう訳ですから石は自由落下しない状況になります。でも台を準備してよじ登るくらいの時間なら、太陽も超新星爆発的な膨張を起こさずに自由落下の実験を眺めていてくれるでしょう。
落とす位置によって違いがあるでしょうか？
落とす時刻によって違いがあるでしょうか？
これは分かりますよね。違いはありません。
落とす高さをグッと高くして、地球からかなり離れた高さから落とすなら、重力の掛かり方が変わりますから違いは出て来ます。でもこの場合はそんなに高い台 (+q) を想定していませんので重力変化は無いものと考えて下さいね。
それと時間に関しては全く問題はないでしょう。もっとも太陽の超新星爆発膨張時刻まで未来 (+p) の話をした場合には違ってきます。ピサの斜塔どころか地球が太陽に飲み込まれてしまう訳ですから石は自由落下しない状況になります。でも台を準備してよじ登るくらいの時間なら、太陽も超新星爆発的な膨張を起こさずに自由落下の実験を眺めていてくれるでしょう。
と言う事で、自由落下運動は高さ・場所・時刻によらず同じように石が落ちて行く事実を前提に、これをグラフ表現する事を考えてみてください。考える点は、１回目の自由落下実験の基準を２回目のそれに強制的に適用すると言う事です。ここがややこしい所。
・自由落下の石の位置 ： １回目の実験は、ピサの斜塔の高さで、これをグラフでは０としている。すると２回目のそれは +q となる。
・時刻 ： １回目の自由落下の時刻 ( １０時 ) が基準となって０としている。すると２回目の時刻は +p となる。
・自由落下の石の位置 ： １回目の実験は、ピサの斜塔の高さで、これをグラフでは０としている。すると２回目のそれは +q となる。
・時刻 ： １回目の自由落下の時刻 ( １０時 ) が基準となって０としている。すると２回目の時刻は +p となる。
グラフ上では、２回目の自由落下の時には余計な +q と +p が、一回目を基準にしてしまっているからこそ付属してきます。でも自由落下は場所や時刻に影響されずに同じように石が落ちて行く訳ですから、この余分な +q と +p を打ち消してやらないといけません。
そう考えると y の値から事前に -q を、また t から事前に -p をしてやる必要がある事が理解できるでしょう。そうする事でグラフが２回目の自由落下も正しく表わせる事が分かります。
でもこの考え方って、一見つじつま合わせにマイナスをした感じがしますよね。でも、つまりはそう言う事だと思います。つじつま合わせ ( 参考書の証明 ) が現実と一致した、という事です。数学の記法と演算法則が現実と一致するので、数学は自然を表現するのに使える道具、と確認できるわけです。私はそう納得をしました。
そう考えると y の値から事前に -q を、また t から事前に -p をしてやる必要がある事が理解できるでしょう。そうする事でグラフが２回目の自由落下も正しく表わせる事が分かります。
でもこの考え方って、一見つじつま合わせにマイナスをした感じがしますよね。でも、つまりはそう言う事だと思います。つじつま合わせ ( 参考書の証明 ) が現実と一致した、という事です。数学の記法と演算法則が現実と一致するので、数学は自然を表現するのに使える道具、と確認できるわけです。私はそう納得をしました。
この考え方、ちょっと強引ですかね。みなさんは納得出来ましたか？
では今日は数学検定の準２級、２次の過去問題をやってみます。
では今日は数学検定の準２級、２次の過去問題をやってみます。
あ、
その前に証明写真を撮って来ないと…忘れるところだった。
応援してね。
千里の道も一歩から。そしてその道は登り坂です。
(ポチッとブログ村のバナーをクリックしてね） 
| 項目 | 昨日の実施状況 | 今日の予定 |
|---|---|---|
| ブログを更新 | ８時５６分 | ８時３０分 |
| そろばんの練習 | できず | ３０分 |
| 数学の学習 | できず | ２次過去問題 |
| + α 学習( LaTeX2ε 、コンテンツ作成など ) | 検定会場の下見 | 証明写真 |
閲覧(4560)
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |
メインメニュー
