みなさん、こんにちは。
今日は「瀬山士郎著、読む数学」と言う書籍を少し読んでみました。

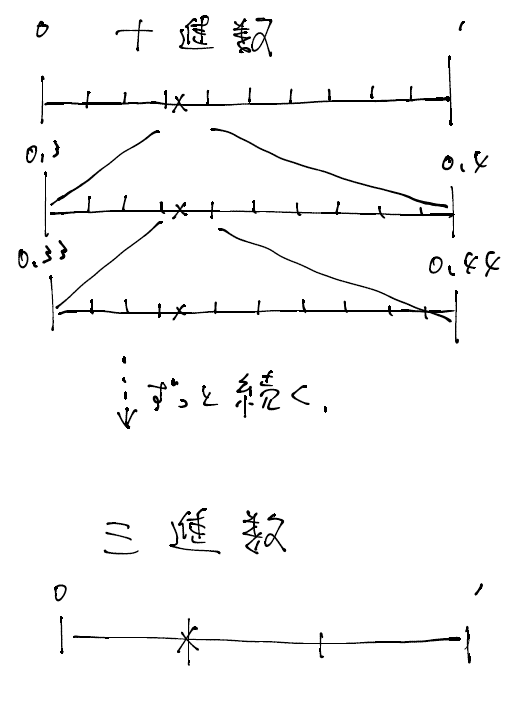
分数と小数と言う章で出てくる分数の説明は頭にスッキリ入ってきます。分数と小数と言う数の表記の違いが解ります。小数とは十進数としての数の表記なのですが、分数は分母を適した数字にする事で、一つの形でスッキリと数字を表記する方法とも考える事が出来ます。例えば 1/3 。これを十進数の小数で表記すると 0.3333… と言う循環小数表記になります。（三進数での小数表記をすると 0.1 と言うシンプルな表記になりますね。）この十進数で小数表記をすると循環小数になってしまう数を、分数の分母に 3 を取ってやると、スッキリとした表記 1/3 となるわけです。

さて、無理数の章を読んだときには、ハタと考えてしまいました。文章を読んでいて突然「循環しない無限小数」と言う表現が出てきます。ギリシャ時代のピタゴラス学派は、すべての量は通約可能（つまり分数表現可能）と考えていた訳ですが、この考えからどのように「循環しない無限小数」と言う数を見つけ出したのでしょうか？無理数の説明をするのならば、循環しない数の発見に付いて書いて貰いたいものです。しかし本書には書かれてはいません。残念です。
続いて 虚数と複素数 と言う章が出てきますが、ここで ”マイナス×マイナス” がプラスになる、と言う事を疑問に思う人も多いと思う、と言う記述があります。自然数から整数へと数の表記が進化する過程で、マイナス表記された数は、実在の物と結び付ける事が難しい数で、一般市民には受け入れられなかったと言う歴史的な経過があるそうです。では、”マイナス×マイナス” がプラスになる、としたほうが数学的に都合が良い、と言う事を見出したのは誰なのでしょう？また、どんな根拠からそう考えたのでしょうか？その根拠のようなものが、後の方の章、あべこべのあべこべは？ に出てきます。この辺は面白いですね。
また、足し算と掛け算の根本的な違いが説明されています。対象物に付いての違いです。足し算は、例えばりんご５０gと距離７ｍを足して５７ｇメートルとする事に意味はありません。しかし掛け算なら、５０ｇ（０．０５ｋｇ）と距離７ｍを掛けると仕事量を表す数として物理学者は扱います。この意味は深いですね。

とりあえず今日はこの辺にしておきましょう。「読む数学」を あべこべのあべこべは？ まで読み進んでくると、そろそろ体の概念が徐々に頭に入ってきます。読み流すだけではなく、手を動かして筆記しながらの方が、この書籍が無駄にならずにすみます。体の概念を理解できそうです。今日はこの辺で。