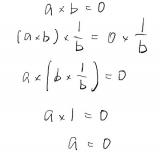みなさん、こんにちは。
今日も「読む数学」を読み進んでいるのですが、ちょっと理解不能な箇所までやってきました。章で言うならば「方程式を解くということ - その１」です。この章の冒頭にこんな事が書かれています。
「ですから、方程式は因数分解できれば解く事ができます。このアイデアを２次方程式に当てはめてみましょう。」と言う部分です。”ですから”と言う言葉が受けているのは、直前の文章です。「 ab = 0 で b ≠ 0 なら、b の逆数 1/b がありますから、両辺に 1/b をかければ、図17 （図と言うよりは式）となり、 a = 0 が得られます。これを数学では、「実数は零因子を持たない」といいます。」
さて、この説明文ですが、私はここから「方程式は因数分解できれば解く事ができます。」と言う結果を受け入れる事が出来ずにいます。（図17 を下に示しておきます）

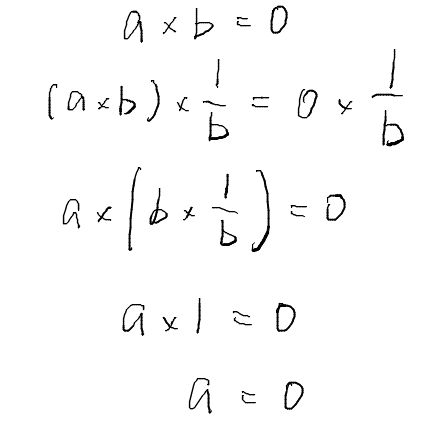
本書「読む数学」のこの章「方程式を解くということ - その１」は、二次方程式の係数と解（α、β）の関係の説明が記述されているのですが、「方程式は因数分解できれば解く事ができます。」が納得できていないので、二次方程式の係数と解（α、β）の関係、の説明がどうも気持ち的に受け入れられないでいます。説明そのものは理解できますが、α、β が唐突に出てきた印象で気持ちが悪いですね。読んだ事のある方、ここの部分、どう思われましたか？ともかくここの章の最後は「この最初の式から、α - β の値がわかれば、α、β を連立方程式として求めることができます。α - β の値を求めることができないでしょうか？」と言う文章で締めくくられていますが、どうしてα - β の値がわかれば、α、β を連立方程式として求めることができのでしょうか？この理由を探してみたのですが、本書の冒頭から「方程式を解くということ - その１」と言う章に至るまでの間に記述されていないと、私は確信しています。

高校時代に確か、同じような二次方程式の係数と解（α、β）の関係と言うのが出てきて、学んだ記憶があります。そう言えばここの所は、当時も納得できなかったところだったと思います。計算自体、やっている事は分かります。しかし話の流れが良くわかりません。「実数は零因子を持たない」と言う事が私は理解できていないのでしょうか？
ともかく、過去の記憶でも、今回の書籍「読む数学」でも、この二次方程式の係数と解の関係は、流れが納得できません。しかしそれはそれとして、次に進んで行きたいと思いますが…。
まぁ今日はこの辺で。またね。