時空 解 さんの日記
2017
9月
21
(木)
10:21
本文
皆さん、おはようございます。時空 解です。
レオンハルト・オイラーの事をちっとも知りませんでした。そりゃあ数学で1番有名な数式の1つ、右下に示した数式を発見したのはオイラーだとは知っていましたが、それだけです。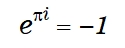
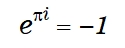
この数式が理解出来ていて、証明もできるとカッコいいですよね。もし自分が学習を重ねて理解できるようになった時には、自分で自分をほめてやりたいと思っています。7年ぐらい前に、書店で「オイラーの贈物―人類の至宝eiπ=-1を学ぶ 」を見かけた時には思わず買ってしまうところでした。買えばこの数式を理解した気になれそうだったからです。でも、この頃から「本当に真剣に理数系に取り組みたい」と言う、自己反省も含めた想いが湧いていたので踏みとどまったんですけどね。
」を見かけた時には思わず買ってしまうところでした。買えばこの数式を理解した気になれそうだったからです。でも、この頃から「本当に真剣に理数系に取り組みたい」と言う、自己反省も含めた想いが湧いていたので踏みとどまったんですけどね。
この数式の理解の先に、まずは円周率・パイや自然底数・イー、それに虚数アイを単独で使いこなしてこそですよね。それからの方が、この最も有名な公式を味わえると言うものです。
「不思議な数eの物語 」の第13章は、この数式の前菜的な味わいが楽しめます。それに、オイラーを取り巻く世の中の状況も分かります。数学の歴史のなかでオイラーは音楽史の中でのモーツァルトのような存在だったとは知りませんでした。それにオイラーに数学を教えたのが、ヨハン・ベルヌーイだったとは驚きです。
」の第13章は、この数式の前菜的な味わいが楽しめます。それに、オイラーを取り巻く世の中の状況も分かります。数学の歴史のなかでオイラーは音楽史の中でのモーツァルトのような存在だったとは知りませんでした。それにオイラーに数学を教えたのが、ヨハン・ベルヌーイだったとは驚きです。
この数式の理解の先に、まずは円周率・パイや自然底数・イー、それに虚数アイを単独で使いこなしてこそですよね。それからの方が、この最も有名な公式を味わえると言うものです。
「不思議な数eの物語
オイラーの残した仕事は数学のみならず、かなり物理学の分野にも及んでいる事も分かります。力学、流体力学、月の運動理論等々。これじゃあまるでニュートンのライバルですよね。書籍には "ライバル" 何て表現は出てきませんが、とにかく数学者と言うよりは理数系の巨人です。
憧れてしまいます。
オイラーの人柄を感じさせるくだりが「不思議な数 e の物語」の第13章、210ページに出て来ます。ちょっと引用してみましょう。
憧れてしまいます。
オイラーの人柄を感じさせるくだりが「不思議な数 e の物語」の第13章、210ページに出て来ます。ちょっと引用してみましょう。
なぜ彼が文字 e を選んだのか? 大方の意見の一致はない。ある意見では、指数の (exponential) という語の最初の文字だからオイラーがそれを選んだという。もう少し本当らしいのが、文字 a, b, c, d は数学のどこかによく出てくるので、アルファベットの中であまり "使われない" 最初の文字を彼は自然に使ったという。時々いわれるように、自分の名前の頭文字だから選んだということはないであろう:彼は非常に控えめな人間で、彼の仲間や学生の業績が認められるように、自分の業績の出版を遅らせることも多かったくらいだから。いずれにせよ、彼の選んだ記号 e は、他の多くの彼の記号同様、世の中に広く受け入れられるようになった。
この書籍の著者、E.マオール氏は自分の数学史研究を通して、オイラーにこんな印象をお持ちのようです。自然底数の記号として、オイラーが自分の頭文字を取って e と付けた、と言うのは間違いだと思っていいでしょう。オイラー自身は純粋に数学の学習をして行く中で、e と言う表記は都合が悪くならなかった、と言う事でしょう。そんな風に彼の数学を学ぶ姿勢を想うと、本当にオイラーに憧れを感じます。オイラーのように理数系とともに生きて行きたいものです。本当にオイラーのように学べると良いのになぁと思いました。彼にとっては数学が子どもにとっての玩具と同じたったのですね。そんなことが次のくだりで分かります。
オイラーは非常に実験好きな数学者だった。子供が玩具で遊ぶように彼は公式で遊んだ --- 何か面白いものが得られるまであらゆる種類の代入をしたりして。その結果が世界を沸かせることになったことも多い。
彼は e^x の無限級数の式 (4) を取り上げて、大胆にも実変数 x のところに虚数の式 ix ( ここで i = √-1 ) を代入した。それまで関数 e^x の定義では、変数 x は常に実数を表していたのだから、これは数学的にものすごく無謀なことであった。実数を虚数で置き換えるなどということは、無意味な記号の遊戯でしかない。しかし、オイラーは彼の公式に確信をもち、無意味なものを意味深いものにしたのだった。
このくだりから数学史上もっとも有名な公式の発見方法が、なんと子供の遊戯心の結果だと分かります。
数学に対して堅苦しいイメージなんてどこにもありませんよね。オイラーが自分でしたい事を思う存分楽しんでいる姿が浮かびます。妄想が先にあります。それを毎日毎日数式に書き表しているうちに、洗練されて行った感じですよね。一般的な数学の学び方とは逆(?)のように思いました。
一般的には、数学的な思考を手に入れるにはまず記号の定義を覚えて、それから演習問題を解いて基礎を固めて、それから応用問題…。そんな感じです。でも、これって、自分の妄想を排除して頭に詰め込むって雰囲気です。私がする妄想なんてのは数学の邪魔になるだけなんですかね?
オイラーは妄想自体が数学的だった、と言えるのかも知れません。頭に浮かぶ妄想を少し整理して記号化すると数学が出来上がってしまう…これはすごいですよ。
数学に対して堅苦しいイメージなんてどこにもありませんよね。オイラーが自分でしたい事を思う存分楽しんでいる姿が浮かびます。妄想が先にあります。それを毎日毎日数式に書き表しているうちに、洗練されて行った感じですよね。一般的な数学の学び方とは逆(?)のように思いました。
一般的には、数学的な思考を手に入れるにはまず記号の定義を覚えて、それから演習問題を解いて基礎を固めて、それから応用問題…。そんな感じです。でも、これって、自分の妄想を排除して頭に詰め込むって雰囲気です。私がする妄想なんてのは数学の邪魔になるだけなんですかね?
オイラーは妄想自体が数学的だった、と言えるのかも知れません。頭に浮かぶ妄想を少し整理して記号化すると数学が出来上がってしまう…これはすごいですよ。
とにかく数学はニュートン、ライプニッツ、そしてオイラーと言う3人の開拓者がいて、その後をジャン・ルロン・ダランベール、ジョゼフ・ルイ・ラグランジュ、オギュスタン・ルイ・コーシーたちが受け継ぐ ( 厳密に証明する ) 形で、今後発展して行くのだそうです。この第13章はそれも実感できて本当に数学史が面白くなります。
では今日も1日を始めます。
応援してね。
では今日も1日を始めます。
応援してね。
千里の道も一歩から。そしてその道は登り坂です。
(ポチッとブログ村のバナーをクリックしてね)![]()
| 項目 | 昨日の実施状況 | 今日の予定 |
|---|---|---|
| ブログを更新 | 7時57分 | 8時30分 |
| そろばんの練習 | できず | 30分 |
| 数学の学習 (青チャートI+A ) | できず | p160 残り |
| 数検の学習 ( ステップアップ ) | できず | ------ |
| + α 学習( LaTeX2ε 、コンテンツ作成など ) | 不思議な数 e の物語 第11、12章 | ------ |
閲覧(15266)
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |





 前の日記
前の日記