50代から理数を学ぶ - 指数が有理数の時に、気になる√a^2

Home > ブログ > 時空解 > 数学 > 指数が有理数の時に、気になる√a^2

時空解さんの日記

2017

10月 10

(火)

10:03

指数が有理数の時に、気になる√a^2

前の日記次の日記

カテゴリー数学

本文

皆さん、おはようございます。時空解です。

昨日、一昨日と、やっと数学検定２級のための学習に取り組み始めました。
なかなか出来なかったのですが、時間が取れなかった事と学習する参考書を決めかねていた事が少し障害になっていました。でも時間は、テレビ番組の予約録画を削減したおかげで取る事ができはじめています。やっとテレビの前に座り込んでしまう習慣から抜け出せそうです。
( 意志が弱い証拠ですけどね

)
参考書は白チャート「新課程チャート式基礎と演習数学 II+B」でよさそうですね。
白チャートは大学の入試対策としては簡単すぎると言うウワサをネットで見かけますが、数学検定に対してはどうでしょうかね…私は丁度いいように思います。３級、準２級と受検してみてそう思います。

そんなこんなで、昨日と一昨日に白チャートの p194 ～ pp201 を学習したのですが、基本事項を押さえには最適な気がしました。５０歳を越えている私には、白チャートを学習した後に青チャートに進む方が、挫折せずに進められそうです。

ところで、白チャートの p194 ～ pp201 は "２４：指数の拡張" と言う節です。指数の取りうる数値が正の整数から有理数の拡張されるんですよね。
中学の時には指数は正の整数までだったように記憶していますが、高校に入ると有理数にまで拡張されて複雑になります。例えば下記のような指数表記の計算をする事になります。

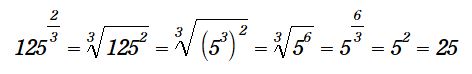
ここで思い出すのが "怖いルート a ２乗" です。ルートを外す時にマイナスをつけるか否か、と言う下記の事です。

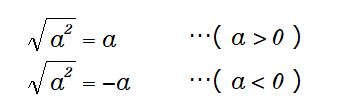
ですから、指数が有理数になると、分母が２、すなわちルートですよね。この時にマイナスを付けるか付けないかを考えなくてはならないのか？心配になったりします。
でもご安心下さい。この "２４：指数の拡張" の部分では a は正の数の場合だけを扱っています。もしかしたら、ひとまず複雑さを回避しているのかも知れませんけどね。
"怖いルート a ２乗" 彷彿とさせるような下記の問題は出て来ますが、この事柄も "怖いルート a ２乗" とは別物です。

混乱しないようにね。私は混乱し掛けましたが…なんとか今は頭の中を整理できました。これについては、また機会があればコンテンツにでもいたします。

( うーむ、コンテンツにする項目が、だんだん増えてきました…夏休みの宿題のようです

)

ま、とにかく今日も１日を始めます。

応援してね。
千里の道も一歩から。そしてその道は登り坂です。
(ポチッとブログ村のバナーをクリックしてね）

毎日の実施・予定表
項目	昨日の実施状況	今日の予定
ブログを更新	９時１７分	８時３０分
そろばんの練習	１０分	３０分
数学の学習 (青チャートI+A )	p187 の途中	p187 ～ p189
数検の学習 ( 白チャート II+B )	p198 ～ p201	p202 ～
+ α 学習( LaTeX2ε 、コンテンツ作成など )	------	------

閲覧(4139)

コメントを書く
コメントを書くにはログインが必要です。