時空 解 さんの日記
2017
11月
3
(金)
08:46
マスペディア 060 ～ 062 - 式の変形も大切 -
前の日記
次の日記
カテゴリー
マスペディア 1000
本文
皆さん、おはようございます。時空 解です。
数学の問題を解いている過程でいろいろな数式を書いて行きますよね。例えば２次不等式を解いている時には、判別式を書いたり、与式を基本形(頂点が分かる形)に変形したり分解形(因数分解)にしたり…。その時にマイナスの符号をどこに書くのか？それを適当に行ったた
めに、答えにたどり着けたなかったと言う事ありませんか？
私は昨日、そんな失敗をしました。
具体的に説明しますと青チャート「改訂版 チャート式 基礎からの 数学I+A」の p203 Exercises 82 の問題です。
めに、答えにたどり着けたなかったと言う事ありませんか？
私は昨日、そんな失敗をしました。
具体的に説明しますと青チャート「改訂版 チャート式 基礎からの 数学I+A」の p203 Exercises 82 の問題です。
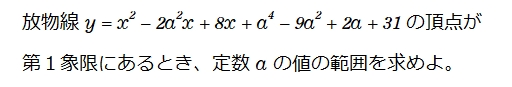
この問題を解くためには、与式を基本形に変形する必要がありますよね。その頂点が第１象限に入るように a を求めればよいのですが…私はこの与式を下記のように変形してしまいました。書籍の変形と私の行った変形を並べて書いてみるとその違いが分かります。
私が行った変形でも、数式的には間違ってはいません。
でもグラフの形が意識できませんよね。
それで何となく下に凸のグラフだと思い込んで a の範囲を求めてしまっています。
式の変形も大切です。グラフの形が意識できるように気を付けましょう。
ウィキペディアの 062 にも似たような問題が載っています。参考に下に書いてみましょう。
ウィキペディアの 062 にも似たような問題が載っています。参考に下に書いてみましょう。
本文 a = b とする。両辺に b を掛けると、ab = b^2 となる。両辺から a^2 を引くと、ab-a^2 = b^2 -a^2 となる。両辺を因数分解すれば、a(b-a) = (b+a)(b-a)。両辺から (b-a) を消して a = b+a となる。a = b と仮定したので、a =2a であり、したがって 1 = 2 となる。
この問題点、分かりますかね？両辺から (b-a) を消す時に間違いがあります。
では今日も１日をはじめます。
応援してね。
千里の道も一歩から。そしてその道は登り坂です。ローマは１日にして成らず、です。
(ポチッとブログ村のバナーをクリックしてね）
| 時間割 | 昨日の実施状況 | 今日の予定 |
|---|---|---|
| １時限目 ブログを投稿 | ８時２６分 | ------ |
| ２時限目 青チャートI+A | p203 ex 81, 82 | p203 ex 83, 84, 85 |
| ３時限目 そろばんの練習 | １０分 | ３０分 |
| ４時限目 白チャート II+B | p212 ～ p213 | p214 ～ p217 |
| 放課後 + α 学習( LaTeX2ε 、コンテンツ作成など ) | ------ |
閲覧(4751)
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |
メインメニュー
