時空 解 さんの日記
2017
11月
20
(月)
08:49
マスペディア 092 ~ 097 - 連分数 -
 前の日記
次の日記
前の日記
次の日記 カテゴリー
マスペディア 1000
カテゴリー
マスペディア 1000
本文
みなさん、おはようございます。時空 解です。
連分数と言うのを皆さんもご存知だと思いますが、これって、高校の数学過程では学ばないですよね?チャート式数学IIIの参考書の初めには分数関数と言う節がありますが、連分数はやはり出て来ません。高校数学の過程では連分数は扱っていないようです。
昨日マスペディアの "092:連分数" と言うトピックを読んで「おや?」とおもいました。と言うのも連分数から、その数字が無理数か否かが判ることが書かれていたからです。
へぇ…それは知らなかった。
これを示したのが、かの有名なオイラーだそうです。
へぇ…それは知らなかった。
これを示したのが、かの有名なオイラーだそうです。
・連分数がずっと続いて ( 無限に続く ) 収束するのであれば、それは無理数を表す
知らなかった。高校でも習わないと思います。
でもこれって、皆さんはどう思われます?と言うのも、これってあまり役には立たない気もしますけどね。
だって考えてもみて下さい。
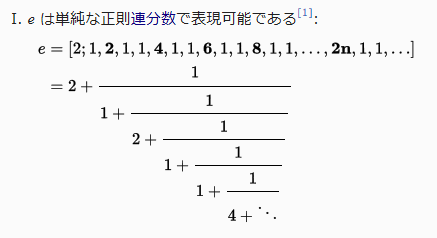
例えば自然定数 e の数をオイラーは連分数で下記のように示して、それをもって「 e は無理数である 」事を示したそうです。
ウィキ、ネイピア数の表現より引用
しかしこの連分数…どうやって得たのでしょうかね?
連分数そのものを得る方法も私には分かりません。
でもこれって、皆さんはどう思われます?と言うのも、これってあまり役には立たない気もしますけどね。
だって考えてもみて下さい。
例えば自然定数 e の数をオイラーは連分数で下記のように示して、それをもって「 e は無理数である 」事を示したそうです。
ウィキ、ネイピア数の表現より引用
しかしこの連分数…どうやって得たのでしょうかね?
連分数そのものを得る方法も私には分かりません。
連分数に関する数学的な知識が全く自分にはないことを感じます。
マスペディアの 095 番目のトピックには、実は " 連分数を作る " と言うトピックがって、その作り方も示されています。単純な分数を連分数に展開する方法が書かれていんですけどね。でもそれをみても全く習った記憶はありませんし、個人的にはあまり興味を持っていなかったのも事実です。
マスペディアの 095 番目のトピックには、実は " 連分数を作る " と言うトピックがって、その作り方も示されています。単純な分数を連分数に展開する方法が書かれていんですけどね。でもそれをみても全く習った記憶はありませんし、個人的にはあまり興味を持っていなかったのも事実です。
でも連分数が無限に続いて、しかもそれが収束するのであれば、それは無理数なのだ、と言う事にはちょっと興味も湧きますよね。それに連分数に関しては優れた先人がいるようです。それがシュリニヴァーサ・ラマヌジャンと言う人です。
この人、かなり有名なインドの数学者のようですね。映画にもなっているようです。
この人、かなり有名なインドの数学者のようですね。映画にもなっているようです。
映画『奇蹟がくれた数式』…( 公式サイトリンク )
うーむ…連分数に興味を持つか、それとも映画の方に興味を持つか…両方に興味を持てばいいですよね。
では、今日も小さな一歩から始めます。
応援してね。
千里の道も一歩から。そしてその道は登り坂です。ローマは1日にして成らず、です。
(ポチッとブログ村のバナーをクリックしてね)![]()
| ★ 習慣作りのための、小さな課題 | ☆ 昨日の実施状況 |
|---|---|
| そろばんの練習5問 (暗算の獲得) ブログ投稿の後 |
パッチトレーニング6:p45 |
| 鉄棒に1回ぶら下がる (ボルダリングの体力獲得) 朝食後 |
腕立て7回、腹筋10回、 |
| チャート式参考書1問 (物理学の数式の理解力の獲得) 午前中の好きな時間 |
青I+A:p206, p207 白II+B:p218, p219 |
閲覧(9098)
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |