時空 解 さんの日記
2017
11月
23
(木)
08:54
本文
みなさん、おはようございます。時空 解です。
やっと対数の底について、そのイメージをつかむ事ができました。
高校時代に対数は、既に理解済みだとばかり思っていたのですが、初歩が分かっていなかったことが判明しました。いやはや、高校時代にいかに学習をサボっていたかです。
高校時代に対数は、既に理解済みだとばかり思っていたのですが、初歩が分かっていなかったことが判明しました。いやはや、高校時代にいかに学習をサボっていたかです。
今年の9月の終わりころから数学検定の2級のために白チャート「新課程 チャート式 基礎と演習 数学 II+B」を学習しています。この参考書の第7章が「指数関数と対数関数」の章です。ここの p220 にある基礎例題 138 (1) で私はつまづきました。
答えをみても納得ができない…そもそも対数の底って、何?
と言う状態に陥りました。
白チャート 数学 II+B の p220 基礎例題 138 と言うのはこんな問題です。
答えをみても納得ができない…そもそも対数の底って、何?
と言う状態に陥りました。
白チャート 数学 II+B の p220 基礎例題 138 と言うのはこんな問題です。
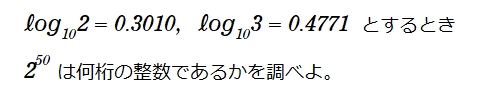
この問題の答えは、次のように始まります。
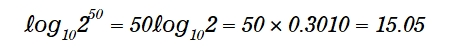
この答えが分らなかったんですよねぇ。問題文に出てくる数値は、2の50乗ですよね。これを log で表すと、底が2でなくてはいけないような気がして、どうして log の10底が納得できませんでした。
でも、どうして納得が出来なかったのか、1日考えていて分かってきました。自分は底とは何かを良く理解してなかったんだと思います。
でも、どうして納得が出来なかったのか、1日考えていて分かってきました。自分は底とは何かを良く理解してなかったんだと思います。
基本例題 138 は何桁の整数であるか?と言う問いかけをしていますが、これが底の理解に役立ちました。例えば2の50乗って、どんな数字でしょう?この数量を2進数表記と10進すう表記を並べて示します。( ついでに10の15乗、16乗も書いておきます。)
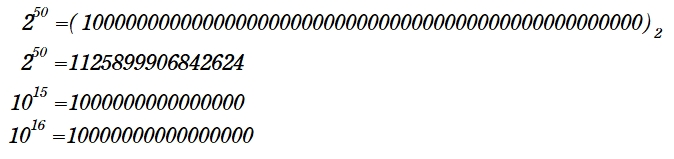
これでなんとなくイメージが湧いてきたのではないでしょうか?
私は上記を観て底が2の時には2進数、底が10の時は10進数と言うイメージが沸いてきました。
10進数を2進数に変換する時の演算方法は、10進数表記の数字を2でどんどん割ってゆきますよね。逆に2進数を10進数にするためには、1桁目は2の1乗、2桁目は2の2乗、3桁目は2の三乗…と言うふうに各桁の数量を求めて、最上位の桁までの数量を合計する訳です。
こんな事を考えて、p220 にある基礎例題 138 (1) の書籍の答えが納得できた次第です。こんな基礎的な事をちゃんとイメージ出来ていなかったんですよね。高校を卒業してはや40年近く…。
ちょっと説明が上手くないかもね…これは個人的な内容ですからね。ごめんなさい。
ま、とにかく今日も小さな一歩から始めます。
応援してね。
千里の道も一歩から。そしてその道は登り坂です。ローマは1日にして成らず、です。
(ポチッとブログ村のバナーをクリックしてね) ![]()
| ★ 習慣作りのための、小さな課題 | ☆ 昨日の実施状況 |
|---|---|
| そろばんの練習5問 (暗算の獲得) ブログ投稿の後 |
(学習方法考え中) |
| 鉄棒に1回ぶら下がる (ボルダリングの体力獲得) 朝食後 |
腕立て5回、腹筋5回、グリップ10×3回 |
| チャート式参考書1問 (物理学の数式の理解力の獲得) 午前中の好きな時間 |
青I+A:できず 白II+B:できず |
閲覧(8696)
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |





 前の日記
前の日記



