50代から理数を学ぶ - ３角比の問題は、やっぱり比を利用して解くべし

Home > ブログ > 時空解 > 数学 > ３角比の問題は、やっぱり比を利用して解くべし

時空解さんの日記

2017

11月 30

(木)

08:53

３角比の問題は、やっぱり比を利用して解くべし

前の日記次の日記

カテゴリー数学

本文

みなさん、おはようございます。時空解です。

昨日青チャート「改訂版チャート式基礎からの数学I+A」の p210 基本問題133 を解いていてハマってしまいました。どうしても答えが合わないのです。
問題を下に示します。( 図形が見にくいですが、ごめんなさい )

この問題の (1) の AD の長さがどうしても答えと一致しませんでした。

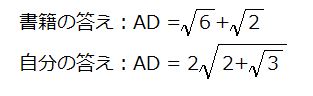
午前中には、この謎を解く事が出来なくて、数学の学習が滞ってしまったんですよね。でも、この２つの数量、皆さんはお気づきですかね、同じなんです。それに気が付くのに時間が掛かってしまいました。それぞれを２乗してみてください。同じ値になります。

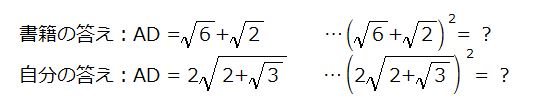
8 + 4√3 になりますよね。

私の値はどのように出したかと言うと、実は３角比を利用せずに、ピタゴラスの定理を使って辺の長さを算出したからこうなってしまったのです。
( 詳細は省きます…ちょっと時間がありませんので…ごめんなさい )

もしも数学検定の時に、上記のような表記をしたらどうなるんでしょうかね？数量的には合っているのに表記的には二重根になっていますので〇は貰えないかな…。
やっはり３角比、キチンと覚えてそれを利用しないと答えが出ない事を実感した昨日でした。

ピタゴラスの定理にこだわって問題を解く私は、柔軟性がありません。素直に比計算を取り入れるべきですね。

参考に、下記のチャート式本書の解答を示しておきます。

では今日も小さな一歩から始めます。

応援してね。
千里の道も一歩から。そしてその道は登り坂です。ローマは１日にして成らず、です。

(ポチッとブログ村のバナーをクリックしてね）

「小さな習慣」の実施状況
★ 習慣作りのための、小さな課題	☆ 昨日の実施状況
そろばんの練習５問 (暗算の獲得) ブログ投稿の後	宮田輝そろばん教室加減算編：練習５(９問) × ６回
鉄棒に１回ぶら下がる (ボルダリングの体力獲得) 朝食後	ぶら下がり１回、斜め懸垂１０回、腕立て１０回、腹筋１０回、グリップ１５回
チャート式参考書１問 (物理学の数式の理解力の獲得) 午前中の好きな時間	青I+A：p210 基本問題 133(1) 白II+B：できず

閲覧(5794)

コメントを書く
コメントを書くにはログインが必要です。