50代から理数を学ぶ - 青チャートI+A 基本例題 135 でつまづいた理由

Home > ブログ > 時空解 > 数学 > 青チャートI+A 基本例題 135 でつまづいた理由

時空解さんの日記

2017

12月 7

(木)

08:58

青チャートI+A 基本例題 135 でつまづいた理由

前の日記次の日記

カテゴリー数学

本文

みなさん、おはようございます。時空解です。

昨日は図書館に行く予定を取りやめにしました。
会社はお休みだったのですが、ボランティア活動の予定が午前中に有った事と、それに青チャートI+A 基本例題 135 にハマっていたんですよね。それで図書館に行って書籍「FOCUS(フォーカス) 集中力 (日経ビジネス人文庫)」を読む時間が無くなってしまったんです。

ハマっていた基本例題 135 とはこんな問題です。

この問題は５分くらい考えても分からなかったので答えを見てみたのですが…それが納得できない、気に入らない！
どうしてもスッキリとしない答えだと、その時には思えたのです。
チャート式の答えはこんな解答です。

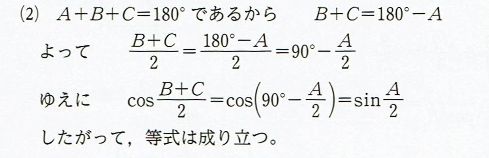
これ、答えを初めて観た時には「数式の変形で証明しているだけだ！本質的な説明は何もない」と思い込んでしまったんです。

昨日さんざん考えて納得できずにいたのですが、今日の朝起きた時には納得していました。

これって、問題の出し方にトラップがありますよね。三角形を使って 180° を連想させるところです。ここで私は幻想を抱きました。
どんな幻想かと言うと「三角形の内角の和は 180° だよな。三角形と sin, cos の関係になにか数学的な本質が隠されているのだろうか？」と深読みしてハマったんです。
( 私の幻想、理解して頂けますかね？もしかしたら誰もこんな幻想抱かないかも知れませんね

)

この問題は ∠A, ∠B, ∠C を使わないで、ダイレクトに定数 a, b, c と言うのを使って出題されていると、途端に簡単な問題になります。
試しに定数 a, b, c を使って問題文を作ってみましたので、読んでみて下さい。

この問題文でしたら直ぐ解ける問題ですよね。

こんな幻想を抱いて、それに１日が振り回されてしまうようでは、まだまだ数学が解っていませんかね…とほほほほ。

今日も小さな一歩から始めます。

応援してね。
千里の道も一歩から。そしてその道は登り坂です。ローマは１日にして成らず、です。

(ポチッとブログ村のバナーをクリックしてね）

「小さな習慣」の実施状況
★ 習慣作りのための、小さな課題	☆ 昨日の実施状況
そろばんの練習５問 (暗算の獲得) ブログ投稿の後	宮田輝そろばん教室加減算編：練習７、８× 通して２回
斜め懸垂１回 (ボルダリングの体力獲得) 朝食後	斜め懸垂５回、腕立て１０回、腹筋１０回、グリップ１０回
チャート式参考書１問 (物理学の数式の理解力の獲得) 午前中の好きな時間	青I+A：p212 基本例題 135 白II+B：できず

閲覧(5069)

コメントを書く
コメントを書くにはログインが必要です。