時空 解 さんの日記
2017
12月
10
(日)
09:02
本文
みなさん、おはようございます。時空 解です。
白チャート「新課程 チャート式 基礎と演習 数学 II+B」の第7章も大詰めを迎えています。章の最後の exercises を解いているところです。ここの2つ目の問題、ex-331 の解法がピンとくるようになると、対数と言う表記方法が良く分かってきたと言えるのではないでしょうか。
私はちょっとつまずきましたけどね。
ex-331 はこんな問題です。
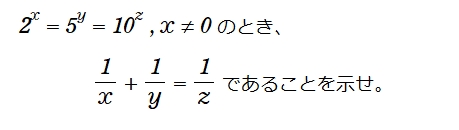
この問題を解くには、上記の与式を常用対数に直して、その式を変形すれば良いのですが、この指数表記をどうして対数表記に変更してもよいのか?それが理解出来ていないとこの問題は解けませんよね。
ちなみに与式を常用対数で表してみましょう。

ここまでくれば、後は丸2の式の両辺を xz で割って、丸3の式の両辺を yz で割って行くと、おのずと答えは出てくると思います。
式の変形はあまり難しい物ではありません。私が思うポイントは指数表記を常用対数表記に変更しても良い事が理解出来ているか、です。これはある量、2を x 乗して表される量を指数表記するか10進数表記でベタに数字を並べて表すか、そのどちらで表記しても、もともとの量は変わらないのと同じ事です。
ある量を、2を x 乗して表すのと、2の x 乗になる量は10を何乗すると2の x 乗の量を示すのか、その表記方法の違いであって、量そのものは同じものを表すのです。
昨日はこの事をちゃんと納得する事に時間が掛かってしまいましたが、日も小さな一歩から始めます。
ある量を、2を x 乗して表すのと、2の x 乗になる量は10を何乗すると2の x 乗の量を示すのか、その表記方法の違いであって、量そのものは同じものを表すのです。
昨日はこの事をちゃんと納得する事に時間が掛かってしまいましたが、日も小さな一歩から始めます。
応援してね。
千里の道も一歩から。そしてその道は登り坂です。ローマは1日にして成らず、です。
(ポチッとブログ村のバナーをクリックしてね) ![]()
| ★ 習慣作りのための、小さな課題 | ☆ 昨日の実施状況 |
|---|---|
| そろばんの練習5問 (暗算の獲得) ブログ投稿の後 |
宮田輝そろばん教室 加減算編:練習7 (1) ~ (5) |
| 斜め懸垂1回 (ボルダリングの体力獲得) 朝食後 |
斜め懸垂5回、腕立て8回、腹筋10回、グリップ10回 |
| チャート式参考書1問 (物理学の数式の理解力の獲得) 午前中の好きな時間 |
青I+A:できず 白II+B:p228 ex-331 |
閲覧(8240)
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |





 前の日記
前の日記



