時空 解 さんの日記
みなさん、こんにちは。
今日も「改訂版 チャート式 解法と演習 数学I + A 数研出版」をチョコチョコとやっていて、「勉強になるなぁ」と思ったものがありました。みなさんは次の式を因数分解できますでしょうか?
出典:「改訂版 チャート式 解法と演習 数学I + A 数研出版」より25ページ、PRACTICE 19 の(2)の問題。
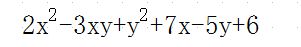
詳しくは出典の書籍そのものを見て貰うと分かると思いますが、個人的にキチンと記憶に留めたいと思い、こうしてブログに書いております。
まず、この多項式は x と y 、共に2次の多項式です。ですので x に着目して整理する方法と y に着目して整理する方法の二通りがありますが、ここでは出典の書籍とは違う、x に付いて整理してみましょう。y の二乗の係数が1なのに対して x の二乗の係数は2なのでちょっと厄介になりますが、お付き合いください。
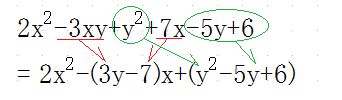
ここで私が注目したのは、-(3y-7)x のところです。括弧の前の - ですね。これは (-3y+7)x とする事もできます。これを頭に片隅に置いておいてください。
さて、次に行なうのは、定数項の因数分解です。定数項と言っても y に付いてみてみれば二次方程式ですので、これを因数分解します。この因数分解は基本的なものなので分かりますね?
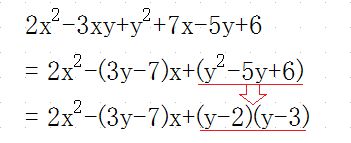
ここまできたら、いよいよこの問題の出題意図の本質です。出題者の意図は、ここからの式の変形を問うところです。今行なった定数項の( y に付いての ) 因数分解が出来る方なら、基本的にここから x に付いての因数分解も出来るはずです。でも x の二乗の係数 2 がちょっと因数分解を複雑にしていますね。また -(3y-7)x としてしまっているので (y-2) , (y-3) の2つから -(3y-7) を作り出すことがちょっと見えにくいです。ですが、ここでは定数項の因数分解が出来ていますので、もう少し式を変形をして因数分解をし易くしてみましょう。
因数分解をするという事は与えられた多項式を最終的には (ax + b)(cx + d) と言う形にする事です。 b と d にこれまでの式を当てはめてみましょう。b と d は分かりますね。当てはめて数式を眺めてみましょう。符号も大切です。+ にするには 正数 × 正数 かまたは 負数 × 負数のどちらかですので、二通りの可能性がありますよね。下にその2つを上下に並べてみました。するとおのずと答えが見えてきませんか?
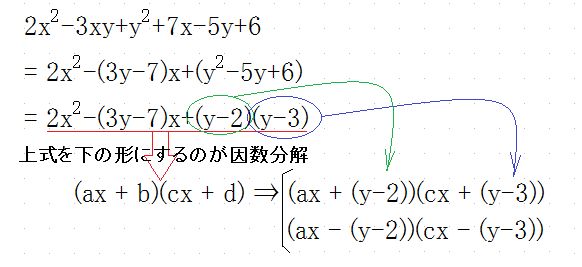
ここまで式を変形して来ると、後は係数の a と c に何を入れるか?です。a と c のどちらかに 2 を入れればいい事は x の二乗係数をみれば分かりますよね。後は -(3y-7)x を (-3y+7)x と書き換えてやれば符号が分かり易くなるでしょう。
ポイントは次の三つです。
(1) x の二乗の係数に付いて、a と c を掛け合わせて 2 になるようにするには、a , c どちらかが 2 でどちらかが 1 と考えられる。
(2) 定数項に付いて、ここは y に付いて因数分解してあるので、因数をそのまま使ってみる。b = (y-2) , d = (y-3) と仮定してみると、次に進みやすい。
(3) x の係数に付いて、-(3y-7)x は (-3y+7)x である事を理解する。
さて、こうすると a , b , c , d の四つに、それぞれに何が入るか分かってきますので、書き並べてみます。
a = 1 かまたは 2
b = (y-2) かまたは -(y-2)
c = 1 かまたは 2
d = (y-3) かまたは -(y-3)
たすき掛けのテクニックは、この a , b , c , d を見やすい形に並べるテクニックといえるでしょう。

個人的に思う事は、たすき掛け と言うテクニックが使いやすいかどうか、と言う事です。因数分解で大切な事は、与式を因数分解が見通せる形に変形する事です。また符号を間違えないです。この2つが出来れば たすき掛け と言うテクニックを利用しなくても、頭の中で因数分解できのではないか、と私は思います。
どうしても因数分解がうまく出来ないのは、括弧を外す時の符号の変わり方、掛け算した後の符号の変わり方、これらがシッカリと分かっていないのではないでしょうか?決して たすき掛け が理解出来ていないから、と言う理由ではないでしょう。
正数 × 正数 = 正数 …例) 2 × 1 = 2
負数 × 負数 = 正数 …例1) -2 × -1 = 2 例2) -(y-2) × -(y-3) = -1 × -(y-2) × -1 × -(y-3) = (y-2)(y-3)
今一度、掛け算をする時の符号に付いて確認をしてみては如何でしょうか?
では今日はこの辺で。
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |





 前の日記
前の日記




