時空 解 さんの日記
2018
2月
19
(月)
10:33
本文
皆さん、おはようございます。時空 解です。
定積分の勉強を一通り終えたところですが、こんなテクニックを学生時代に習ったかなぁ…と思う問題がありました。ですので、今日はその事に付いて書いてみましょう。
問題は 新課程 チャート式基礎と演習数学2+B の p272 基礎例題 171 (2) から、下記の通りです。
の p272 基礎例題 171 (2) から、下記の通りです。
等式 \( \displaystyle\int_a^xf(t)dt=x^2+2x-3 \) を満たす関数 \( f(x) \)、および定数 \( a \) の値を求めよ。
この問題のポイントは2つあるんですけどね。その2つとも高校時代に習った覚えがないのです。
でもこの問題、きっと良く出題される問題だと思います。何故かと言うと、微分も出てくるし解析的な考え方も必要だからです。総合力をためすのに持って来いの問題のように私は思います。
さて、この問題を解くためには2つ、やらなくてはいけない事があります。
まず1つ目。\( f(x) \) を求める必要があります。
私は最初、間違えて \( x^2+2x-3 \) を積分してしまいましたけど、これではダメですね。\( \displaystyle\int_a^xdt \) は \( t \) に付いて積分しろ!と言う記号なので、それと等しい \( x^2+2x-3 \) は積分されて出てきている数式と言う事です。ですから \( f(x) \) は \( x^2+2x-3 \) を微分しなくては求められません。
と言う事で与式の両辺を微分すると下記のようになります。
\( f(x)=2x+2 \)
これで求める関数 \( f(x) \) は求められました。
次は2つ目。\( a \) を求めるのですが、この求め方が私にとっては妙技でした。\( \displaystyle\int_a^xf(t)dt \) の上端についている変数 \( x \) に\( a \) を代入するんですねぇ~。そうすると\[ \displaystyle\int_a^af(t)dt=0 \]ですよね。つまり\[ 0=a^2+2a-3 \]となるのです。
これを因数分解すれば\[ (a-1)(a+3)=0 \]ですから \( a=1,-3 \) となって \( a \) が求められました。
これで問題は解けたわけですが…ちょっと疑問に想いませんか?どうして定数 \( a \) が定まってしまうのか疑問じゃありませんか?
と言う事で私はグラフを書いてみた次第です。
まぁグラフを書いたと言っても、カルキングソフトと言う数式エディタを使えばすぐにグラフを書けますので、それを利用しているだけですけどね。
それでカルキングソフトで \( x^2+2x-3 \) と \( 2x+2 \) をグラフ上に一緒に示します。
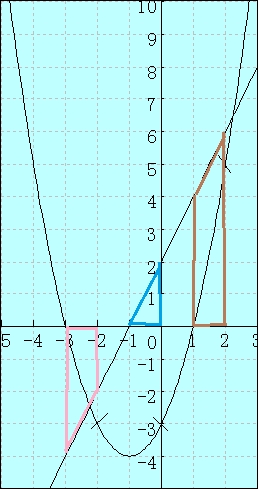
こうしてみると確かに \( a \) は \( -3 \) もしくは \( 1 \) でなくてはならない事が見て取れます。それを一緒に見て行きましょう。
ピンク色で囲ったところは、□の数を数えて貰うと分かりますよね。\( -3 \) です。そして双曲線 \( x^2+2x-3 \) の \( x=-2 \) の時が確かに \( -3 \) になっている事が分かります。これがすなわち\[ \displaystyle \int_{-3}^{-2}(2x+2)dt \]ですよね。
これと同じように茶色のところを見てみても \( a=1 \) の時には成り立っている事が分かります。
では例えば \( a=-1 \) ではどうでしょう?
グラブ上で言うと青色の三角の部分です。この面積は1ですよね。\[ \displaystyle \int_{-1}^0(2x+2)dt=1 \]ですが、双曲線の方は \( -3 \) を示していますよね。成り立っていません。
いかがでしょうか、皆さん。この問題は私に取っては意味を理解するのにちょっと手こずる問題でした。直ぐに左に示したグラフをイメージできたでしょうかね。
では今日も1日を始めます。
だいぶ遅くなっちゃったけどね。
定積分の勉強を一通り終えたところですが、こんなテクニックを学生時代に習ったかなぁ…と思う問題がありました。ですので、今日はその事に付いて書いてみましょう。
問題は 新課程 チャート式基礎と演習数学2+B
等式 \( \displaystyle\int_a^xf(t)dt=x^2+2x-3 \) を満たす関数 \( f(x) \)、および定数 \( a \) の値を求めよ。
この問題のポイントは2つあるんですけどね。その2つとも高校時代に習った覚えがないのです。
でもこの問題、きっと良く出題される問題だと思います。何故かと言うと、微分も出てくるし解析的な考え方も必要だからです。総合力をためすのに持って来いの問題のように私は思います。
さて、この問題を解くためには2つ、やらなくてはいけない事があります。
まず1つ目。\( f(x) \) を求める必要があります。
私は最初、間違えて \( x^2+2x-3 \) を積分してしまいましたけど、これではダメですね。\( \displaystyle\int_a^xdt \) は \( t \) に付いて積分しろ!と言う記号なので、それと等しい \( x^2+2x-3 \) は積分されて出てきている数式と言う事です。ですから \( f(x) \) は \( x^2+2x-3 \) を微分しなくては求められません。
と言う事で与式の両辺を微分すると下記のようになります。
\( f(x)=2x+2 \)
これで求める関数 \( f(x) \) は求められました。
次は2つ目。\( a \) を求めるのですが、この求め方が私にとっては妙技でした。\( \displaystyle\int_a^xf(t)dt \) の上端についている変数 \( x \) に\( a \) を代入するんですねぇ~。そうすると\[ \displaystyle\int_a^af(t)dt=0 \]ですよね。つまり\[ 0=a^2+2a-3 \]となるのです。
これを因数分解すれば\[ (a-1)(a+3)=0 \]ですから \( a=1,-3 \) となって \( a \) が求められました。
これで問題は解けたわけですが…ちょっと疑問に想いませんか?どうして定数 \( a \) が定まってしまうのか疑問じゃありませんか?
と言う事で私はグラフを書いてみた次第です。
まぁグラフを書いたと言っても、カルキングソフトと言う数式エディタを使えばすぐにグラフを書けますので、それを利用しているだけですけどね。
それでカルキングソフトで \( x^2+2x-3 \) と \( 2x+2 \) をグラフ上に一緒に示します。

こうしてみると確かに \( a \) は \( -3 \) もしくは \( 1 \) でなくてはならない事が見て取れます。それを一緒に見て行きましょう。
ピンク色で囲ったところは、□の数を数えて貰うと分かりますよね。\( -3 \) です。そして双曲線 \( x^2+2x-3 \) の \( x=-2 \) の時が確かに \( -3 \) になっている事が分かります。これがすなわち\[ \displaystyle \int_{-3}^{-2}(2x+2)dt \]ですよね。
これと同じように茶色のところを見てみても \( a=1 \) の時には成り立っている事が分かります。
では例えば \( a=-1 \) ではどうでしょう?
グラブ上で言うと青色の三角の部分です。この面積は1ですよね。\[ \displaystyle \int_{-1}^0(2x+2)dt=1 \]ですが、双曲線の方は \( -3 \) を示していますよね。成り立っていません。
いかがでしょうか、皆さん。この問題は私に取っては意味を理解するのにちょっと手こずる問題でした。直ぐに左に示したグラフをイメージできたでしょうかね。
では今日も1日を始めます。
だいぶ遅くなっちゃったけどね。
応援してね。
千里の道も一歩から。そしてその道は登り坂です。ローマは1日にして成らず、です。
(ポチッとブログ村のバナーをクリックしてね) ![]()
![]()
| ★ 習慣作りのための、小さな課題 | ☆ 昨日の実施状況 |
|---|---|
| そろばんの練習5問 (暗算の獲得) ブログ投稿後 |
宮田 輝 そろばん教室 練習問題9 7回 |
| 斜め懸垂1回 (ボルダリングの体力獲得) 朝食前 |
斜め懸垂10回、グリップ20回、腕立て10回、腹筋10回 |
| チャート式参考書1問 (物理学の数式の理解力の獲得) 朝食後9時から |
白II+B:p273 青I+A:できず |
| 心の筋トレ (集中力の獲得) 習慣を実行するにあたって |
今朝・7時に布団から出る:7時38分 --- ブログの投稿 --- 昨日・朝食は台所で摂って2階へ:〇 昨日・机に座ったら、直ぐに学習用具を開く:× 昨日・理数の解法を楽しむ:〇 昨日・夜食も台所で摂って2階に:〇 昨日・夜は23時に布団に入る:23時19分 |
閲覧(9379)
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |





 前の日記
前の日記



